Johannes Kepler: Jak w wolnych chwilach odkryć tajemnicę kosmosu? (1595)

W lipcu 1595 roku Johannes Kepler był dwudziestotrzyletnim nauczycielem w luterańskiej szkole w Grazu w Styrii. Przysłano go tam z Tybingi, gdzie się uczył i miał nadzieję zostać teologiem. Był jednak biedny i korzystał z książęcego stypendium, musiał więc pojechać do Grazu, kiedy tylko zwierzchnicy tak postanowili. Nawiasem mówiąc, Wirtembergia z czasów Keplera miała znakomity system edukacyjny, w którym biedny, lecz uzdolniony młodzieniec mógł przejść przez szkoły wszystkich stopni, nie płacąc ani za naukę, ani za utrzymanie w bursie. A był to przecież XVI wiek! Rządzący kierowali się głównie względami religijnymi: potrzeba było jak najwięcej wykształconych teologów luterańskich, ale uczono porządnie, choć raczej w duchu konserwatywnym.
Kepler podczas studiów zainteresował się astronomią, i to heliocentryczną – jego nauczyciel Michael Mästlin był bowiem jednym z niewielu zwolenników Kopernika. Pół wieku po ukazaniu się dzieła toruńskiego astronoma, zwolenników jego nauk można było policzyć na palcach jednej ręki. Nie było mowy o żadnym przewrocie kopernikańskim, ponieważ prawie nikt nie wierzył, iż Ziemia naprawdę się porusza, a przedstawiony przez Kopernika system to coś więcej niż ćwiczenie z zakresu matematyki stosowanej, bez konsekwencji kosmologicznych.
Kepler w Grazu wciąż chciał myśleć, że po kilku latach wróci do Tybingi i dokończy studia teologiczne. Stało się inaczej, pochłonęła go astronomia (i astrologia), a i władze w Tybindze niezbyt chyba chciały mieć Keplera z powrotem. Był prawdziwie pobożny, ale jak często się to zdarza takim ludziom, nie był ostrożny w wypowiadaniu poglądów i mówił to, w co wierzył. A zwierzchnikom chodziło raczej o ujednoliconą doktrynę, nie o prywatne przemyślenia. Posłuszeństwo ceniono wyżej niż błyskotliwość i gorący zapał.
Uczył w Grazu przedmiotów matematycznych, co obejmowało astrologię. Młody nauczyciel lubił opowiadać nie tylko, co myśli, ale także jak do tego doszedł. Dzięki temu wiemy, że zajął się latem 1595 roku astronomią kopernikańską: „Kiedy pragnąłem dobrze i zgodnie z kierunkiem pracy spędzić czas wolny od zajęć” [ten i poniższe cytaty za: J. Kepler, Tajemnica kosmosu, przeł. M. Skrzypczak i E. Zakrzewska-Gębka, Ossolineum 1972, nieznacznie zmienione].
W astronomii Kopernika proporcje orbit planetarnych wyznaczone są przez obserwacje. Jeśli nawet system heliocentryczny był nieco prostszy, to nasuwało się pytanie: czemu sfery planet są takiej a nie innej wielkości? Jeśli była to rzeczywista architektura kosmosu, to czym kierował się boski Architekt?

A były głównie trzy problemy, których przyczyn, dlaczego jest tak a nie inaczej szukałem, a mianowicie liczba, wielkość i ruch sfer. Odwagi dodała mi owa idealna zgodność pozostających w bezruchu Słońca, gwiazd stałych i przestrzeni pośredniej, z Bogiem-Ojcem, Synem i Duchem Świętym. (…) Początkowo rozważałem zagadnienie w zależności od liczb i zastanawiałem się, czy jedna sfera może być dwa, trzy, cztery razy większa od drugiej w teorii Kopernika. Wiele czasu poświęciłem tej pracy jakby zabawie, ponieważ nie ukazywała się żadna zgodność ani samych proporcji, ani jej przyrostu. Nie osiągnąłem z tego żadnych korzyści; wbiłem sobie jednak głęboko w pamięć odległości, tak jak zostały podane przez Kopernika. (…) Wydaje się, jakoby ruch zawsze podążał za odległością i że gdzie istniał wielki przeskok między sferami, to podobny przeskok występował także między ich ruchami.

Warto zauważyć, że już wtedy Kepler usiłował dociekać, jaka jest zależność między okresem obrotu a wielkością sfery (czyli orbity) planety – w roku 1618 odkrył ścisłe prawo rządzące tą zależnością, zwane dziś III prawem Keplera. Był to więc jeden z problemów, nad którymi rozmyślał całe życie. Młody nauczyciel był pomysłowy: próbował np. umieścić między Marsem a Jowiszem nową planetę, a inną między Wenus i Merkurym, sprawdzając, czy wtedy proporcje jakoś orbit dadzą się lepiej zrozumieć. Teoretycznie było możliwe, że krążą tam gdzieś jakieś niewielkie i nie wykryte planety. Między Marsem a Jowiszem rzeczywiście krąży wiele takich ciał, znanych jako planetoidy. Badał też inne pomysły. Wszystko na próżno.

Prawie całe lato straciłem na tych męczarniach. W końcu przy jakiejś drobnej okazji przybliżyłem się do sedna sprawy. Uznałem, że z bożej łaski udało mi się znaleźć przypadkowo to, czego wcześniej nie mogłem osiągnąć pracą. Uwierzyłem w to tym bardziej, że zawsze prosiłem Boga, aby pozwolił ziścić się moim zamiarom, jeśli Kopernik miał słuszność. W dniu 19 lipca 1595 r., zamierzając pokazać moim słuchaczom skok wielkich koniunkcji przez osiem znaków (…) wpisałem w jedno koło wiele trójkątów, albo quasi-trójkątów, tak aby koniec jednego był początkiem drugiego.

 

Rysunek przedstawia koniunkcje Jowisza i Saturna na tle znaków zodiaku – jest więc całkowicie abstrakcyjny. Koniunkcje te powtarzają się w odległości około jednej trzeciej zodiaku, jeśli połączyć te punkty liniami, uzyskuje się rysunek Keplera. Sądzono, że te koniunkcje mają ważne znaczenie astrologiczne, stąd taki temat lekcji. Kepler dostrzegł jednak w tym rysunku coś innego:

Teraz mamy trójkąt wpisany między dwa okręgi. Mogłyby to być sfery Saturna i Jowisza – dwóch planet najdalszych od Słońca. Może więc kwadrat należy wpisać między sferę Jowisza i Marsa itd. Pojawia się jednak kłopot: mamy tylko sześć planet (znanych ówcześnie), a wieloboków foremnych jest nieskończenie wiele. Konstrukcja powinna wyjaśniać, czemu jest akurat sześć planet, a nie np. 120. Wtedy przypomniał sobie Kepler XIII księgę Elementów Euklidesa. Grecki matematyk dowodzi tam, że istnieje dokładnie pięć wielościanów foremnych, czyli takich, że wszystkie ich ściany są jednakowymi wielobokami foremnymi.

Rysunek: Wikipedia, Максим Пе

W Platońskim Timajosie wielościany te powiązane są z pięcioma elementami, z których zbudowany jest kosmos: sześcian z ziemią, dwudziestościan z wodą, ośmiościan z powietrzem, czworościan z ogniem, a dwunastościan z eterem wypełniającym wszechświat. Była to wówczas śmiała spekulacja oparta na najnowszej matematyce Teajteta, jednego z uczniów Platona. Teraz Kepler znalazł dla tych wielościanów nowe zastosowanie. Należało między sześć sfer planetarnych wpisać owe pięć brył platońskich.

Jest to konstrukcja zawrotna: pewien głęboki fakt matematyczny został powiązany z układem planetarnym – dla Keplera nasz układ był jedyny we wszechświecie, a Stwórca myślał językiem geometrii. Pozostawało tylko zająć się szczegółami: kolejnością brył, kwestią, jak cienkie powinny być sfery planetarne, czy ich środek liczyć od środka orbity Ziemi, czy od Słońca. Rozwiązana została tajemnica kopernikańskiego kosmosu. I taki właśnie tytuł: Tajemnica kosmosu, nosiło dziełko opublikowane przez Keplera w następnym roku. Zwracał się w nim do czytelnika: „Nie znajdziesz nowych i nieznanych planet, jak te, o których mówiłem nieco wyżej – nie zdobyłem się na taką zuchwałość. Znajdziesz te stare (…) tak jednak utwierdzone, że mógłbyś odpowiedzieć rolnikowi pytającemu, na jakich hakach zawieszone jest niebo, że nie osuwa się”.

Nasz Układ Słoneczny okazał się raczej dziełem dość chaotycznych procesów niż wytworem Platońskiego demiurga. Proporcje orbit nie wynikają z żadnej ścisłej matematyki, Kepler się mylił. Był to szczęśliwy błąd – uskrzydlony odkryciem, pogodził się z tym, że nie zostanie teologiem i zajął się astronomią, co z pewnością wyszło na dobre nauce. Do końca życia wierzył, że wielościany mają coś wspólnego z uporządkowaniem sfer planetarnych, umysłowi zawsze trudno się rozstać z ulubionymi chimerami. W następstwie hipotezy wielościanowej Kepler zajął się szczegółami ruchów planet – to na tej drodze czekały go wielkie odkrycia.

Wielościany foremne związane są ze skończonymi podgrupami grupy obrotów w przestrzeni trójwymiarowej. Można o nich poczytać w książce M. Zakrzewskiego, Algebra z geometrią, Oficyna Wydawnicza GiS 2015. Bardziej popularne są piękne i znakomicie ilustrowane odczyty Hermanna Weyla, wielkiego matematyka i kolegi Einsteina z Zurychu i Princeton, pt. Symetria, PWN 1960, wznowione przez wydawnictwo Prószyński i S-ka w 1997 r.

Eudoksos i jego hippopede: początki greckiej astronomii matematycznej (pierwsza poł. IV w. p.n.e.)

Urodzony w Knidos, w Azji Mniejszej (dzisiejsza Turcja), Eudoksos syn Aischinesa był lekarzem, astronomem, geometrą i prawodawcą we własnym mieście – zestaw umiejętności zbliżony do tych, z których niemal dwa tysiące lat później słynął, choć w innych proporcjach, także Mikołaj Kopernik. Spośród wszystkich rozrzuconych po Śródziemnomorzu kolonii greckich w polityce, sztuce, filozofii nadal przodowały Ateny, które jednak wchodziły w fazę zmierzchu po złotym wieku. Na zewnątrz murów miejskich Platon, uczeń Sokratesa, założył swoją słynną Akademię. Jednym z jego uczniów był Eudoksos. Pisze Diogenes Laertios:

Kiedy miał bowiem dwadzieścia trzy lata i żył w trudnych warunkach materialnych, znęcony sławą sokratyków udał się do Aten wraz z lekarzem Teomedontem, na którego utrzymaniu pozostawał (a jak twierdzili niektórzy był jego kochankiem). Gdy wylądowali w Pireusie, zamieszkał tam i co dzień udawał się do Aten, gdzie słuchał wykładów sofistów, po czym wracał do swego mieszkania. Po upływie dwóch miesięcy wrócił do ojczyzny… (przeł. B. Kupis)

Był to początek licznych podróży Eudoksosa: spędził jakiś czas w Egipcie, w Kyzikos, na Sycylii, a także na dworze Mauzolosa (to na jego cześć wzniesiono pierwsze Mauzoleum) i znowu w Atenach. Był wybitnym matematykiem, jego teoria proporcji pozwoliła w sposób ścisły włączyć do matematyki liczby niewymierne, wskazuje się nieraz na jej podobieństwo z pracami Richarda Dedekinda i Karla Weierstrassa w drugiej połowie XIX wieku, kiedy także stanął przed matematykami problem umocnienia podstaw ich dyscypliny. Wiele wyników Eudoksosa trafiło później do Elementów Euklidesa.

Nas interesuje tutaj jedno konkretne odkrycie, a właściwie pewien błyskotliwy pomysł geometryczny Eudoksosa. Pamiętajmy, jesteśmy w IV w. p.n.e., nieznana jest jeszcze spora część geometrii, obserwacje astronomiczne rzadko bywają ścisłe, nie ma zresztą dokładnych zegarów, co w astronomii jest konieczne. Znamy natomiast wygląd nocnego nieba, znają go wszyscy. Wiemy, że gwiazdy krążą wokół obserwatora w rytmie doby gwiazdowej (nieco krótszej niż słoneczna). Łatwo to wyjaśnić: przymocowane są do sztywnej sfery, która wiruje w rytmie dobowym wokół Ziemi. Nietrudno też wyjaśnić roczny ruch Słońca na niebie: najwyraźniej okrąża ono w ciągu roku koło nachylone względem równika sfery niebieskiej. Punkt O to Ziemia, mała w porównaniu z kosmosem.

Podobny krok można uczynić i dla planet. Pojawia się tu wszakże komplikacja: otóż zazwyczaj poruszają się one z zachodu na wschód względem gwiazd, lecz od czasu do czasu zawracają na jakiś czas i w efekcie zakreślają na niebie pętlę albo zygzak.

Eudoksos wpadł na pomysł, jak taki ruch wsteczny, jak nazywają go astronomowie, dodać do „zwykłego” ruchu prostego. Potrzebne są dwie dodatkowe sfery poruszające się z taką samą prędkością kątową, lecz niemal przeciwnie. Tzn. gdyby osie obrotu obu tych sfer się pokrywały, oba obroty znosiłyby się wzajemnie. Gdy jednak osie te będą nachylone do siebie pod pewnym kątem, punkt na sferze – nasza planeta – zakreśli leżącą ósemkę, znak podobny do . Mamy więc pewien ruch średni plus zakreślanie ósemki, którą starożytni nazywali hippopede – pęta końskie. Pętlę tego rodzaju zakładano koniom, aby nie oddaliły się samowolnie z miejsca parkowania.

Jako znakomity matematyk Eudoksos z pewnością potrafił udowodnić, że hippopede jest przecięciem sfery z wewnętrznie do niej stycznym walcem.

Możemy śmiało uznać, że tak narodziła się astronomia matematyczna, jak też i matematyczna fizyka, bo z czasem metody matematyki przeniknęły także do badań ziemskiej rzeczywistości. Eudoksos zainspirowany był naukami Platona, który sądził, że geometria ujmuje pewną rzeczywistość idealną, dostępną umysłowi i doskonalszą niż ta zmysłowa. Nie znamy reakcji Platona na pomysł Eudoksosa, znamy jednak reakcję jego ucznia Arystotelesa. Uznał on, że należy włączyć osiągnięcia Eudoksosa do wizji świata. Postąpił trochę tak, jak współczesny filozof, który zastanawia się nad sensem Wielkiego Wybuchu albo Standardowego Modelu Cząstek. Tę filozoficzną wersję modelu Eudoksosa znamy wszyscy jako zestaw koncentrycznych sfer: obraz panujący przez następne dwa tysiące lat.

 

Rysunek z Cosmographii Petera Apiana z XVI wieku, a więc książki współczesnej Kopernikowi. Tutaj można obejrzeć większe obrazki. W średniowieczu dodano do tego obrazka dodatkowe sfery: wody firmamentu ponad gwiazdami (zgodnie z Biblią, gdzie wody znajdowały się ponad niebem, aby mógł padać deszcz), a także zlokalizowano niebo teologiczne jako obszar na zewnątrz fizycznych sfer (Arystoteles sądził, że cały kosmos jest kulą i nie ma sensu mówić o obszarze na zewnątrz). U Apiana mamy: „Niebo empirejskie, siedzibę Boga oraz wszystkich zbawionych”.

W samej astronomii żywot hippopede i modelu kosmosu złożonego z koncentrycznych sfer był znacznie krótszy. Mimo całej błyskotliwości, hippopede nie wystarcza do opisania tego, co widzimy. Np. Mars jest wyraźnie znacznie jaśniejszy podczas ruchu wstecznego niż podczas ruchu prostego, co sugeruje zmiany odległości od Ziemi. Ponadto tory planet nie powtarzają się, więc nieuchronnie należy ten model skomplikować. Zrobili to Apoloniusz i Ptolemeusz. Najtrwalsza okazała się jednak idea matematycznego objaśnienia wszechświata. W tym sensie dzisiejsi badacze tacy, jak Roger Penrose czy Stephen Hawking, a wcześniej Johannes Kepler czy Isaac Newton, są kontynuatorami idei Eudoksosa, że za pomocą matematyki zrozumieć można wszechświat.

Na koniec przyjrzymy się geometrii modelu. Planeta obraca się najpierw o kąt od do wokół osi , a potem o taki sam kąt wokół osi od do .

Zrzutujmy ten ruch na płaszczyznę .

Otrzymujemy następującą sytuację: Okrąg, po którym porusza się zrzutowany na płaszczyznę jest elipsą. Punkt możemy skonstruować jako rzut punktu na większym okręgu prostopadle do osi na tę elipsę.  Trójkąt jest prostokątny i obrót o kąt wokół osi przeprowadza go w trójkąt . Punkt leży więc na okręgu przechodzącym przez punkty , a kąt jest jako kąt środkowy równy . Ponieważ jest rzutem na płaszczyznę , więc leży na powierzchni bocznej walca o promieniu . Punkt leży też oczywiście na sferze.

Josef Loschmidt i wielkość cząsteczek powietrza (1865)

Richard Feynman pisał, że gdyby cała obecna nauka miała ulec zniszczeniu w jakimś kataklizmie i można było ocalić tylko jedno zdanie, to powinno ono brzmieć: „Wszystko składa się z atomów – małych cząstek, poruszających się bezładnie, przyciągających się, gdy są od siebie nieco oddalone, odpychających się zaś, gdy je zbytnio ścieśnić”.

Pomysł istnienia takich cząstek, jak i ich nazwę: atomy, czyli „niepodzielne” (a to zaprzeczenie, tomos – cięty, tnący, dzielący się na części, stąd np. określenia anatomia i tomografia) zawdzięczamy starożytnym Grekom Leucypowi i Demokrytowi. Rzeczy zbudowane są z atomów jak słowa z liter. Pisma atomistów były już w starożytności atakowane za wizję świata bez bogów, poddanego tylko konieczności. Istniała w nim tylko materia, nawet dusze, czyli zasady ruchu, miały być bowiem materialne.

Żyjący w I w. p.n.e. Rzymianin Lukrecjusz opisał tę wizję w długim i dydaktycznym, i o dziwo poetycko wybitnym, poemacie heksametrem. Lukrecjusz był epikurejczykiem, a więc nie tylko atomistą, lecz także wyznawcą etyki opartej na wartościach doczesnych – bogowie nie zajmują się bowiem ludźmi, a ci powinni sami zadbać o swe szczęście, żyć tak, by o ile to możliwe szukać przyjemności i unikać cierpienia. Etyka epikurejska była rozsądna i wyważona, obce im było wszelkie zatracanie się w pogoni za szczęściem, jak i nadużycia zmysłowe. Ceniono natomiast proste przyjemności i czystą radość życia. Atomizm, objaśniając funkcjonowanie świata, miał dopomóc ludziom w uwolnieniu się od lęku przed śmiercią, zemstą bogów i wizją wiecznego cierpienia po śmierci. Z tego względu już w starożytności epikureizm uznawano za filozofię bezbożną.

Kanoniczny obraz atomizmu to drobinki pyłu wirujące w smudze światła słonecznego. W mikroskali tak miały wyglądać wszystkie zjawiska: wiecznie poruszające się i zderzające atomy. Niezmienność ukryta pod zmieniającą się powierzchnią zjawisk.

Bo spojrzyj jeno, gdy promienie słonecznego światła wedrą się i rozleją po mrocznym domostwie! Zobaczysz w tym promiennym snopie wiele maleńkich ciałek, mieszających się w próżni na wiele sposobów. Jakoby w wiekuistej wojnie staczają potyczki i bitwy, walczą całymi hufcami bez chwili spoczynku, w utrapieniu ustawicznych skupień i rozłączeń. Z tego więc możesz zmiarkować, jak wygląda wieczne miotanie się zarodków rzeczy w ogromie próżni, o ile mała rzecz może dać przykład i tropy poznania wielkich. A jeszcze z tego powodu winieneś zwrócić baczniejszą uwagę na owe ciałka, co wichrzą dostrzegalnie w promieniach słonecznych, że takie wichrzenia zdradzają nadto istnienie tajnych i niewidocznych ruchów materii. Zobaczysz tam bowiem, że wiele ciałek, podrażnionych niewidzialnymi ciosami, zmienia drogę i w tył zawraca po odepchnięciu, to tu to tam, na wszystkie zewsząd strony. (Lukrecjusz, ks. II, przeł. A. Krokiewicz) (*)

Po Rzymianach rzeczywiście wydarzył się kataklizm: starożytna cywilizacja upadła, o atomistach wiedziano niewiele więcej niż to, że Arystoteles ich zwalczał. Ich pisma przepadły. Półtora tysiąca lat później, w 1417 r., osobliwy poemat Lukrecjusza odnalazł humanista i „łowca rękopisów”, papieski sekretarz, Poggio Bracciolini, prawdopodobnie w alzackim klasztorze w Murbach, gdzie dobrzy mnisi nie bardzo rozumieli, co za tekst przechowują na półkach. Przez następne wieki poemat był wielokrotnie wydawany i tłumaczony na języki narodowe, w tym na język angielski po raz pierwszy w XVII wieku. Atomizm nadal wzbudzał lęk: zderzające się atomy trudno było pogodzić z Opatrznością, choć niektórzy uczeni, jak Isaac Newton, potrafili zbudować jakąś chwiejną syntezę obu koncepcji. Jego Bóg był jednak surowym Pantokratorem, Wszechwładnym Ojcem, nie znoszącym sprzeciwu.

Benjamin Franklin, bystry i zaradny drukarz z Filadelfii, jeden z ojców założycieli Stanów Zjednoczonych, nie był zawodowym uczonym, nigdy nie miał takich ambicji. Ze swoim sposobem uprawiania nauki mieścił się zresztą znakomicie w tradycji Towarzystwa Królewskiego, które od samego początku zrzeszało przede wszystkim hobbystów i amatorów: lekarzy, pastorów, wiejskich dżentelmenów, podróżników (co zresztą nie przeszkadzało niektórym z nich dokonać ważnych odkryć).

Interesował się on legendarnym zjawiskiem uśmierzania fal przez rozlewanie oleju i poczynił w związku z tym pewne obserwacje. Wyniki doświadczeń Franklina przedstawione zostały w listach wymienianych między nim a medykiem Williamem Brownriggiem oraz wielebnym Farishem, opublikowanych w „Philosophical Transactions”. Po opisaniu swych wcześniejszych obserwacji podczas podróży morskich Franklin relacjonuje:

Będąc w Clapham, gdzie na wspólnych gruntach znajduje się duży staw, i widząc pewnego dnia, iż jego powierzchnia jest bardzo wzburzona wiatrem, przyniosłem ampułkę oleju i wylałem go trochę na wodę. Widziałem, jak rozprzestrzenia się on ze zdumiewającą szybkością po powierzchni; lecz efekt uspokojenia fal nie powstał, gdyż zastosowałem go początkowo po nawietrznej stronie stawu, gdzie fale były największe i wiatr zwiewał mój olej z powrotem na brzeg. Następnie przeszedłem na stronę zawietrzną, gdzie [fale] się tworzyły, i tam olej, w ilości nie większej niż łyżeczka do herbaty, spowodował natychmiastowe uspokojenie na obszarze wielu jardów kwadratowych; poszerzało się ono stopniowo w zadziwiający sposób, aż dotarło do przeciwnego brzegu, czyniąc jedną czwartą stawu, jakieś pół akra, gładką jak zwierciadło.

Franklin zwrócił uwagę na zdumiewająco wielką powierzchnię plamy oleju na wodzie.

Jeśli upuścić kroplę oleju na gładki marmurowy stół czy na zwierciadło, kropla pozostanie na swoim miejscu, tylko nieznacznie się rozszerzając. Lecz gdy upuścić ją na wodę, rozprzestrzenia się na wiele stóp dookoła i staje się tak cienka, że na znacznym obszarze wytwarza barwy pryzmatyczne, a jeszcze dalej staje się tak cienka, że aż niewidoczna, prócz efektu wygładzania fal na znacznie większych odległościach. Wydaje się, że wzajemne odpychanie cząsteczek pojawia się, kiedy tylko dotkną one wody, i że jest ono tak silne, iż działa także na inne ciała znajdujące się na powierzchni, takie jak słomki, liście, wióry itp., zmuszając je do ustąpienia ze wszystkich stron wokół kropli niczym centrum i pozostawiając duży pusty obszar.

Te obserwacje z roku 1773 zostały podjęte po przeszło stu latach przez wybitnego fizyka brytyjskiego lorda Rayleigha, w celu oszacowania rozmiarów cząsteczek oleju. Jeśli przyjąć, że zgodnie z tym, co spostrzegł Franklin, 2 cm³ oleju rozprzestrzeniają się na powierzchni pół akra, czyli 2000 m², otrzymujemy grubość warstwy równą 1 nm. Wiemy obecnie, że olej tworzy na wodzie warstwę o grubości jednej cząsteczki, więc dane te pozwalają oszacować jej rozmiary. Amerykanin nie wykonał jednak tego rachunku, zadowolił się samą obserwacją.

Atomy zaczęły odgrywać bardziej konkretną rolę dzięki chemii Johna Daltona. W drugiej połowie XIX wieku fizycy tacy, jak James Clerk Maxwell i Rudolf Clausius, zauważyli, że obraz zderzających się molekuł można rozwinąć w teorię kinetyczną gazów. Ciśnienie gazu było objaśniane bombardowaniem ścianek naczynia przez jego cząsteczki poruszające się z ogromnymi prędkościami (rzędu prędkości dźwięku w danym gazie). Teoria ta dawała też zaskakujący wynik: otóż lepkość gazu miała być niezależna od jego gęstości. Maxwell z pomocą żony przeprowadził odpowiednie pomiary, które potwierdziły teorię. Znając lepkość, można było obliczyć średnią drogę swobodną cząsteczek. W powietrzu w warunkach normalnych wynosiła ona wg Maxwella .

Pierwszym fizykiem, który wyznaczył wielkość cząsteczek powietrza, był Josef Loschmidt. Urodzony w 1821 r. niedaleko Karlsbadu (dziś Karlovy Vary) w rodzinie chłopskiej, przeszedł długą i nieoczywistą drogę do działalności naukowej, pracował nad zagadnieniami z pogranicza matematyki i psychologii, skończył studia politechniczne w Wiedniu, założył własną firmę, zbankrutował, potem był nauczycielem i dopiero w 1866 r., a więc dobrze po czterdziestce, zaczął uczyć na Uniwersytecie Wiedeńskim, zrobił doktorat i został profesorem. Z młodym Ludwigiem Boltzmannem chodzili na koncerty i spierali się o Eroikę Beethovena.

Praca dotycząca wielkości cząsteczek była pionierska, do dziś mówi się czasem o liczbie Loschmidta (liczba cząsteczek gazu w 1 cm³ w warunkach normalnych), choć sam uczony nie podał jej wartości w swej pracy. Znany był związek między koncentracją , drogą swobodną oraz przekrojem czynnym cząsteczek :

Zakładając, że cząsteczki są kuliste o średnicy , przekrój czynny zapisać można jako pole powierzchni koła o  średnicy (cząsteczki zderzają się, gdy ich środki są w odległości od siebie). Nie znamy koncentracji ani promienia, potrzebne jest więc jeszcze jedno równanie. Loschmidt przyjął, że w stanie ciekłym cząsteczki upakowane są ciasno, a więc porównując objętość grama cieczy do objętości gazu, możemy określić, jaką część objętości gazu zajmują cząsteczki. Mamy więc

Wyznaczając z obu równań , otrzymujemy

W przypadku powietrza, które nie było jeszcze wtedy skroplone (Wróblewski, Olszewski 1883 r.), Loschmidt wyznaczył wartość pośrednio, uzyskując 0,000866 zamiast 0,0014. Wyznaczona przez niego średnica cząsteczki równa była około 1 nm, a więc nieco za dużo. Drugą nieznaną wielkością w tym układzie równań jest koncentracja powietrza w warunkach normalnych, czyli właśnie liczba Loschmidta.

Ludwig Boltzmann po śmierci przyjaciela wygłosił wspomnienie o nim. Znalazły się w nim słowa:

Ciało Loschmidta rozpadło się już na atomy: na ile konkretnie atomów – możemy obliczyć, korzystając z ustanowionych przez niego zasad. I aby w przemówieniu dotyczącym fizyka eksperymentatora, nie obyło się bez pokazu, poprosiłem, by napisano tę liczbę na tablicy: . (***)

Sprawa istnienia atomów nie była wszakże wtedy przesądzona. Boltzmann wierzył w ich istnienie, ale Ernst Mach, fizyk i filozof z tego samego uniwersytetu w nie nie wierzył. Dopiero doświadczenia Jeana Perrina przypieczętowały tę kwestię już w XX wieku.

(*) W przekładzie wierszowanym fragment ten brzmi następująco:

Przypatrz się bowiem promieniom słonecznym, kiedy wtargnęły

Do domu i rozlewają światło po ciemnych zakątkach:

Zobaczysz w strumieniu światła bez liku drobniutkich pyłków,

Które mieszają się z sobą w próżni na wiele sposobów;

I jakby ścierał się zastęp z zastępem w wieczystej wojnie,

Wiodąc potyczki i bitwy bez jednej chwili wytchnienia,

Tak one na przemian ciągle to schodzą się, to rozchodzą;

Gdyś widział to, możesz sobie przedstawić, jak w wielkiej próżni

Miotają się bez żadnego przestanku zarodki rzeczy –

O ile rzecz drobna może wystarczyć za podobiznę

Rzeczy ogromnych i wskazać drogę do ich zrozumienia.

Z jednego jeszcze powodu winieneś zwrócić uwagę

Na pyłki, które widomie się kłębią w promieniach słońca:

Ich pomieszanie oznacza, że również wewnątrz materii

Istnieją ruchy, tajemne dla oczu, niedostrzegalne.

Zobaczysz, że wiele pyłków, niedostrzegalnie rażonych,

Odmienia drogę, że wiele pchniętych do tyłu zawraca,

Pędzą to w jedną, to w drugą stronę, we wszystkich kierunkach.

(przeł. G. Żurek, T. Lucretius Carus, O naturze rzeczy, ks. II, w. 113-141)

(**) Sens tego równania jest bardzo prosty: cząsteczka poruszając się, zakreśla w ruchu miedzy zderzeniami walec o objętości , średnia liczba cząsteczke w takim walcu równa jest i powinna być rzędu jedności, dokładny współczynnik dają ściślejsze rozważania, nb. Loschmidt użył w tym miejscu współczynnika wynikającego z pracy Clausiusa.

(***) Ciało ludzkie liczy jakieś atomów. Boltzmann nie był tu zbyt precyzyjny.

 

Czemu Ptolemeusz był wielkim astronomem?

Klaudiusz Ptolemeusz – jak wskazuje rzymskie Klaudiusz i greckie Ptolemeusz – był Grekiem żyjącym w czasach imperium rzymskiego. Pracował w kosmopolitycznej, handlowej i uczonej Aleksandrii, jednym z wielu miast założonych przez Aleksandra Macedońskiego. Zdobywca światów umarł młodo, lecz poszerzył zasięg greckiej kultury. Egipska Aleksandria stała się głównym ośrodkiem nauki tworzonej w języku greckim: Muzeum albo Musejon, przybytek muz, był czymś w rodzaju instytutu naukowego ze słynną biblioteką, obserwatorium astronomicznym, ogrodami botanicznymi i zoologicznymi. Od Euklidesa przez Apoloniusza, Hipparcha do Ptolemeusza rozwijały się tam nauki matematyczne. Sam Ptolemeusz jest autorem Geografii, traktatów o muzyce, optyce i astrologii oraz podstawowego dzieła astronomicznego Mathēmatikē Syntaxis („Zbiór matematyczny”– bezbarwne tytuły nie są wynalazkiem współczesnych uczonych), znanego też jako Megiste („Największy”), co przeszło w arabskie al-majisṭī, z czego wzięła się używana od średniowiecza do dziś nazwa Almagest. Już sama historia tego tytułu pokazuje skomplikowane dzieje przekazywania wiedzy greckiej do nowożytnej Europy.

Mapa świata wg Geografii Ptolemeusza narysowana w XV wieku (Wikimedia Commons)

Mapka rozpowszechnienia Almagestu do czasów Kopernika (В.А. Бронштэн, Клавдий Птолемей, 1988)

Z czasem dzieło Ptolemeusza zawędrowało nawet dalej niż sięgały zdobycze Aleksandra Macedońskiego, bo aż do Indii i do Chin. Co było w nim tak niezwykłego, że tłumaczono je na różne języki, pracowicie kopiowano, a potem drukowano? Almagest i Elementy to najważniejsze dzieła greckie dotyczące nauk ścisłych. Elementy były popularne aż do końca XIX wieku, ponieważ zawierały podstawy geometrii i nadawały się do nauczania w szkołach. Jednak późniejsi uczeni greccy, jak Archimedes, Apoloniusz czy Pappus znacznie powiększyli wiedzę matematyczną. Inaczej w przypadku Almagestu: stanowił on szczyt osiągnięć greckich i można odpowiedzialnie powiedzieć, że dopiero Johannes Kepler posunął dalej sztukę rozumienia ruchów planet, przekraczając poziom osiągnięty przez Ptolemeusza. A więc od II w.n.e. aż do początku wieku XVII ludzkość nie miała lepszej astronomii niż Ptolemeuszowa. Zmieniały się mapy polityczne, wierzenia, religie, języki, kultury, a dzieło Ptolemeusza wciąż stanowiło punkt odniesienia, szczyt kiedyś już zdobyty, ale wciąż trudny do ponownego zdobycia.

Teorie wykładane w Almageście nie są autorstwa Ptolemeusza. Konstrukcje geometryczne zawierające złożenia ruchów po okręgach zastosował już Apoloniusz. Wiele ważnych obserwacji dokonał Hipparch. Do Ptolemeusza jednak należy synteza całej tradycji i sformułowanie jej w postaci pewnego systemu wiedzy. Korzystał z nagromadzonych obserwacji, sam był aktywnym obserwatorem, poprawił też zastane rozwiązania. Almagest pozwala dla danej daty i godziny znaleźć położenie na niebie Słońca, Księżyca, a także pięciu znanych wówczas planet. Sądzono, że położenia te mają wpływ na los człowieka – astrologia była głównym motywem badań astronomicznych. Można wszakże sądzić, że matematyczne umysły w rodzaju Apoloniusza czy Ptolemeusza tak czy owak zgłębiałyby ruchy planet. Są one bowiem powtarzalne, ale niezupełnie, ich usytuowanie nigdy się naprawdę nie powtarza, choć w oczywisty sposób zawiera pewne cykle. Sądzę, że i bez astrologii ruch planet byłby wyzwaniem. Astrologia była raczej koniecznym dopowiedzeniem: skoro świat jest tak urządzony, że owe boskie ciała krążą w zawiły sposób po niebie, to musi to w jakiś sposób dotyczyć także naszego losu. Oczywiście, przeskok od matematyki do cech charakteru czy obliczenia daty odpowiedniej  np. na ślub był logicznie i empirycznie wadliwy, ale i zrozumiały: ludzie zawsze starają się znaleźć w świecie przede wszystkim to, co może ich dotyczyć. Egocentryzm jest postawą jeszcze bardziej naturalną niż geocentryzm.

Podstawowa idea modeli planetarnych była prosta. Mamy dwa okręgi: większy o środku (deferent) i mniejszy o środku (epicykl). Wektor obraca się, unosząc epicykl, planeta znajduje się na jego obwodzie, na końcu wektora . Ziemia spoczywa w punkcie . Ruch zachodzi tu w jednej płaszczyźnie. Planety znajdują się na niebie zawsze w pobliżu ekliptyki, czyli rzutu płaszczyzny orbity Ziemi na sferą niebieską. A więc w pierwszym przybliżeniu możemy ich ruchy rzutować na tę jedną płaszczyznę – dla nas jest to płaszczyzna orbity Ziemi, dla starożytnych była to płaszczyzna orbity Słońca. Dzięki temu model płaski może opisywać najważniejszą część ruchu planet. Odchyleniami od ekliptyki zajmowano się również, ale było to niejako drugie przybliżenie, którego szczegóły tutaj sobie darujemy. Warto pamietać, że dopiero Johannes Kepler wpadł na pomysł, iż orbity planet leżą w płaszczyznach, które przecinają się w Słońcu. Nie wiedzieli o tym starożytni ani Mikołaj Kopernik.

Zazwyczaj dominuje ruch po deferencie w lewo i planeta porusza się względem gwiazd z zachodu na wschód. Czasem jednak zatrzymuje się i zaczyna poruszać się ruchem wstecznym, ze wschodu na zachód. Potem znów wraca do ruchu prostego, tzn. z zachodu na wschód. Pętla w naszym przybliżeniu powinna być spłaszczona: zostaje tylko zmieniający się ruch w płaszczyźnie ekliptyki. Epicykl potrzebny był właśnie do tego, by odtwarzać ruch wsteczny planety.

 

Ptolemeusz ani jego koledzy nie wiedzieli prawie nic o odległościach planet. Wiadomo wprawdzie, że np. Mars jest najjaśniejszy w środku swego ruchu wstecznego, kiedy jest na niebie po przeciwnej stronie niż Słońce (jest w opozycji do Słońca, mówią astronomowie). Sugeruje to, że powinien wtedy być bliżej, ale epicykl ma taki, a nie inny kształt z przyczyn estetyczno-filozoficznych: co się porusza w cyklu, powinno się poruszać koliście. Kierunki przewidywane przez ten model są  opisane prawidłowo – tyle wiedział Ptolemeusz. Fakt, że również i odległości są opisane prawidłowo, jest dodatkową cechą modelu, z czego pierwszy zdał sobie sprawę Kopernik. Jeśli znamy kierunki obu wektorów , to znamy i wektor położenia planety

Pierwszy z wektorów po prawej stronie jest stały. Zauważył bowiem Hipparch, że Ziemię lepiej jest odsunąć nieco od środka deferentu (dla każdej planety inaczej i w innym kierunku). Dwa ruchome wektory obracają się jednostajnie i ich kierunek dla danej chwili można zawsze obliczyć.

I w tym miejscu pojawia się z pozoru drobne ulepszenie autorstwa Ptolemeusza: ekwant. Miał on do dyspozycji więcej obserwacji niż Hipparch, minęły między nimi stulecia – postęp naukowy był wówczas niesłychanie powolny. Zresztą po Ptolemeuszu w zasadzie postępu nie było przez następne tysiąc pięćset lat. Piszę w zasadzie, ponieważ astronomowie islamscy i potem chrześcijańscy aż do Kopernika i do końca XVI wieku wprowadzali rozmaite udoskonalenia, które jednak niczego nie poprawiały. Na początku XVII wieku nadal najlepszą teorią była ta Ptolemeuszowa. Jej błędy dla Marsa zwykle nie przekraczały 1°.

Błędy w położeniach Marsa według efemeryd Origanusa (Ptolemeusz) i Keplera (źródło: O. Gingerich, Johannes Kepler and the Rudolphine Tables, „Sky and Telescope”, December, 1971, s. 328). Warto może dodać, że oprócz uczonych islamskich i Kopernika nikt nie dodawał epicykli do epicykli. Spotyka się czasem powiedzenie, że dalsze poprawianie jakiejś niezbyt udanej teorii to dodawanie kolejnych epicykli. Otóż takiego dodawania kolejnych epicykli w historii nie było. Teoria Ptolemeusza zestarzała się, by tak rzec moralnie (heliocentryzm itd.), ale matematycznie i pod względem zgodności z obserwacjami – wcale. Dalsze epicykle nie były potrzebne.

Gdy obserwuje się ruchy Marsa (w tym przypadku widać to najwyraźniej), okazuje się, że pętle ruchu wstecznego mają różne wielkości w różnych częściach nieba. Planeta w opozycji porusza się też raz szybciej, raz wolniej. Odsunięcie Ziemi od środka deferentu nie wystarczy. Dlatego Ptolemeusz wprowadził kontrowersyjne, ale znakomite rozwiązanie. Przyjął mianowicie, że punkt   porusza się jednostajnie nie względem środka okręgu , lecz względem pewnego innego punktu (zwanego ekwantem) i położonego po drugiej stronie środka deferentu tak, że .

Teraz kąt jest proporcjonalny do czasu, planeta nadal krąży jednostajnie po epicyklu (kąt jest proporcjonalny do czasu). Teoria przewiduje następujące ruchy Marsa:

Z punktu widzenia obserwatora ziemskiego Mars zatacza skomplikowane spirale: ich pętle odpowiadają ruchowi wstecznemu. Widzimy, że ich wielkość zależy od miejsca, w którym planeta znajdzie się najbliżej Ziemi: opozycje bliskie ujemnemu kierunkowi osi x odpowiadają mniejszej odległości planety od Ziemi niż opozycje po przeciwnej stronie ekliptyki. Dobrą zgodność ilościową otrzymujemy, uwzględniając ekwant – kontrowersyjne, jako się rzekło, rozwiązanie Ptolemeusza. Popatrzmy jeszcze na pętle Wenus:

Na drugim wykresie widać, że tor planety podwaja się po ośmiu latach. Zjawisko to wynika ze szczególnej wartości stosunku okresów obiegu Ziemi i Wenus wokół Słońca i nie ma dotąd przekonującego wyjaśnienia.

Jak dobrym przybliżeniem rzeczywistości jest ekwant? W przypadku Marsa deferent odpowiada orbicie planety, epicykl – orbicie Ziemi. Ograniczmy się do deferentu.

Położenie punktu , czyli heliocentrycznie rzecz biorąc, planety, dane jest odległością i kątem . Kąt jest proporcjonalny do czasu. Można łatwo obliczyć, że w modelu Ptolemeusza dla , otrzymujemy (pomijając wyrazy z potęgami wyższymi niż druga):

Porównajmy to z wynikami dla ruchu keplerowskiego po elipsie z tą samą dokładnością:

Zatem błędy równe są

Nawet dla Marsa, gdy , błędy są mniejsze niż , a . Teoria Ptolemeusza jest więc rewelacyjnie dokładna, biorąc pod uwagę ówczesny stan wiedzy i dokładność pomiarów. O takiej dokładności marzył Mikołaj Kopernik, ale jej nie osiągnął. Problemem była tu nie teoria, lecz dobór parametrów modelu na podstawie obserwacji.

Jeszcze na koniec powiedzmy, dlaczego pomysł z ekwantami był kontrowersyjny przez 1500 lat, zanim Kepler nie zrozumiał, jak świetne jest to przybliżenie rzeczywistych ruchów i nie poszedł dalej. Teoria geometryczna była znakomita, ale nie bardzo sobie wyobrażano, jak niebiosa realizują taki ruch. Planety były, jak wierzono, unoszone przez pewne sfery, rodzaj mechanizmu zegarowego. Można wyobrazić sobie, że ów mechanizm zawiera mniejsze i większe kółka. Można było nawet umieścić Ziemię ekscentrycznie. Jednak obrót, który nie jest jednostajny względem swego środka , ale względem innego punktu , wydawał się mechanicznie niewykonalny. Ludzie rozumieją zawsze tyle, ile potrafią wykonać albo przynajmniej wyobrazić sobie jako pewną idealną wersję tego, co działa tu na Ziemi. Ptolemeusz wykazał się niezwykłą odwagą, przedkładając zgodność z obserwacjami nad fizyczną realizację. Jego ekwant był ogniskiem elipsy w zarodku: w jednym ognisku mamy Słońce, wokół drugiego ogniska, które jest puste, prędkość kątowa jest niemal stała.

Pokażemy jeszcze, jak w dzisiejszym języku opisać można Ptolemeuszowe tory planet i jak wyznaczyć w funkcji , czyli czasu.

Z trójkąta COE i twierdzenia sinusów dostajemy

Wektor położenia planety jest zatem równy:

gdzie jest kątem CP z osią x. Oba kąty zmieniają się liniowo z czasem:

 

gdzie są okresami obiegu deferentu i epicyklu. Linie zakreślane przez narysowane zostały wyżej dla przypadku Marsa i Wenus.

Z rysunku tego łatwo wyznaczyć w funkcji , czyli czasu.

Mamy bowiem kolejno:

Ostatecznie więc

Odległość znajdujemy z tw. Pitagorasa. Wynik dla ruchu keplerowskiego znaleźć można w podręcznikach mechaniki niebios, np. klasycznej książce F.R. Moultona. Nasza konwencja jest zgodna z tradycją dawnej astronomii: mierzymy kąty od apogeum. Obecnie panuje zwyczaj mierzenia ich od perigeum/perihelium, różnią się więc o 180º, co daje nieco inne znaki.

Elementy – Euklides (ok. 300 p.npe.)

Myślimy często o starożytnej Grecji jako o cywilizacji, która dała nam filozofię, teatr, poezję, historię, sztukę, logikę, demokrację. Mniej dostrzegane są początki nauk ścisłych, które, wbrew wszelkiemu prawdopodobieństwu, osiągnęły u Greków niezwykle wysoki poziom. Dwa najważniejsze dzieła, Elementy i Almagest, powstały w Aleksandrii, pierwsze na początku świetności miasta, drugie już pod jej koniec. Oddzielone od siebie ponad czterema wiekami, skondensowały w sobie to, co najlepsze w starożytnym dorobku. A bez greckiej geometrii i astronomii nie do pomyślenia byłaby późniejsza nauka islamska, a także praca Mikołaja Kopernika i jego następców prowadząca do rewolucji naukowej XVII wieku.

Tekst Elementów, podzielony na trzynaście ksiąg, obejmuje w sposób systematyczny najważniejsze osiągnięcia matematyki greckiej przed Archimedesem. Napisane około roku 300 p.n.e. dzieło było przez wieki kopiowane zarówno w greckim oryginale, jak i w przekładach na hebrajski, arabski i łacinę, a od 1482 roku zaczęło ukazywać się drukiem w niezliczonych wydaniach książkowych, które liczbą ustępują tylko wydaniom Biblii. Aż do początku XIX wieku znano tekst Euklidesa jedynie w redakcji Teona z Aleksandrii, uczonego z IV w.n.e., ojca Hypatii. W 1808 r. François Peyrard, pierwszy bibliotekarz École Polytechnique w Paryżu, odkrył, iż rękopis Elementów zrabowany z Watykanu przez Napoleona (Vaticanus graecus 190, zwany też P) jest wcześniejszą wersją dzieła. Stała się ona później podstawą definitywnego wydania opracowanego przez duńskiego filologa Johana Ludviga Heiberga.

[Vaticanus graecus 190]

Dzieło Euklidesa nie było pierwszym noszącym ten tytuł, szybko stało się jednak klasyczne, czego pośrednim dowodem jest fakt, że nie zachowały się niemal żadne wcześniejsze teksty matematyczne – w czasach gdy kopiowanie książek było kosztowne i pracochłonne, następowała swoista selekcja naturalna rękopisów, w której te bardziej przydatne wypierały mniej użyteczne. Elementy są najwcześniejszym zachowanym greckim traktatem poświęconym matematyce, ponieważ stanowią one podręcznik, z którego można nauczyć się podstaw matematyki. Stosowane były w tej funkcji nie tylko w starożytności, ale i w czasach późniejszych aż po dziewiętnasty wiek.

Zadziwiająco mało wiemy o autorze tekstu, nawet jego istnienie podawano w wątpliwość, argumentując, że dzieło jest niejednorodne i różne jego księgi wykazują rozmaity stopień dojrzałości. Na ogół sądzi się jednak, że Euklides działał i prawdopodobnie także urodził się w Aleksandrii, mieście niedługo wcześniej założonym przez Aleksandra Wielkiego i przez długie wieki stanowiącym ośrodek nauki i kultury greckiej. Według Proklosa, neoplatończyka z V w.n.e., Euklides żył za panowania Ptolemeusza I i był młodszy niż krąg uczniów Platona, a starszy od Archimedesa i Eratostenesa. Miał być platonikiem i z tego powodu dzieło jego kulminowało konstrukcją i omówieniem pięciu brył platońskich, znanych z Timajosa. Euklidesa nie uważano nigdy za oryginalnego twórcę, sądzono, że zebrał on i usystematyzował osiągniecia poprzedników, w szczególności Eudoksosa i Teajteta. Elementy nie są jednak prostą kompilacją znanego już materiału, lecz próbą zbudowania dedukcyjnego systemu wiedzy matematycznej. Możliwe, że tak jak i w późniejszej historii matematyki, po okresach szybkich postępów następowały okresy systematyzacji i porządkowania wiedzy i Elementy są świadectwem takiego dążenia. Choć odkrycia późniejszych matematyków, takich jak Archimedes, Apoloniusz i Pappus, znacznie wykroczyły poza problematykę Elementów, dzieło to pozostało najszerzej używanym podręcznikiem w historii. Jego znaczenie nie ogranicza się do matematyki: dedukcyjny system wiedzy stał się ideałem wielu późniejszych filozofów i uczonych. W naukach ścisłych aż do dziś uważa się możliwość ustrukturyzowania wykładu na wzór greckiej geometrii za ważny sprawdzian dojrzałości danej dyscypliny. Wprowadzając postulaty, z których następnie wyprowadzamy twierdzenia, osiągamy pojęciową jasność i większą przejrzystość konstrukcji myślowych, musimy bowiem uświadomić sobie jasno przyjęte założenia.

Pamiętać też należy, iż grecka geometria nie była traktowana jako abstrakcyjna gra logiczna, lecz jako teoria wywodząca się z obserwacji dotyczących ciał w przestrzeni, stanowiła więc i nadal stanowi (wraz z nieeklidesowymi rozszerzeniami) podstawę fizyki. Można więc traktować ją jako pierwszą matematyczną teorię fizyczną. Kiedy niedługo później Archimedes w podobny sposób ujmował zasady równowagi ciał, rozszerzał niejako geometrię, tworząc zarazem pierwszą fizykę matematyczną.

Poniżej skoncentrujemy się na przedstawieniu metody postępowania Euklidesa, ograniczając się do tego, co było znane i czytane najszerzej i nie ograniczało się tylko do samej matematyki. Aksjomatyczna konstrukcja wiedzy jest osiągnięciem greckim nie mniejszym niż demokratyczne rządy albo rzeźba. Dzięki Euklidesowi nigdy już nie stracono z oczu, przynajmniej w kręgu śródziemnomorskim, owej metody uzyskiwania zdań niezbitych i pewnych. Jeśli prawdą jest, że (jak ujął to Alfred North Whitehead) filozofia europejska stanowi ciąg przypisów do Platona, to z niemniejszą dozą słuszności powiedzieć można, że nauki ścisłe – fizyka w nie mniejszym stopniu niż matematyka – stanowią rozbudowany komentarz do Elementów Euklidesa.

Każda z ksiąg (albo grup ksiąg) poprzedzona jest definicjami. Księga pierwsza zaczyna się od wymienienia pięciu postulatów geometrii oraz pięciu ogólniejszych prawidłowości odnoszących się do tego, co Euklides nazywa wielkościami – może tu chodzić (jak czytelnik dowiaduje się przy okazji kolejnych twierdzeń) o długość odcinka, wielkość kąta, pole powierzchni czy objętość pewnych brył. Następnie z owych dziesięciu założeń wyprowadzane są kolejne twierdzenia oraz konstrukcje. Księgi I-IV oraz VI, XI-XIII poświęcone są geometrii, sięga V zawiera wykład teorii proporcji Eudoksosa (odgrywały one w matematyce greckiej rolę dzisiejszych liczb rzeczywistych), księgi VII-IX dotyczą arytmetyki, w księdze X dyskutowane są rozmaite rodzaje liczb niewymiernych, zawsze jednak traktowanych jako proporcje długości pewnych odcinków. Ostatnia księga XIII kończy się twierdzeniem, że istnieje dokładnie pięć brył platońskich (sześcian oraz foremne: czworościan, ośmiościan, dwunastościan i dwudziestościan).

Podejście Euklidesa niewątpliwie wiele zawdzięcza istniejącej już tradycji matematycznej, a także platońskiemu rozróżnieniu między przedmiotami postrzeganymi przez zmysły a bytami idealnymi: korzystając z rysunków, traktuje je tylko jako pomoc w wyobrażeniu sobie, jak mają się do siebie idealne figury geometryczne. Koncepcję uporządkowania wiedzy, zaczynając od założeń, których prawdziwość przyjmuje się bez dowodu, znaleźć można u Arystotelesa, nie wiadomo jednak, czy występuje tu jakaś bezpośrednia zależność, czy tylko wspólna tradycja filozoficzna. Geometria stała się pierwszą wyspecjalizowaną dziedziną wiedzy, uprawianą nie ze względów praktycznych, lecz dla niej samej. Wysokie mniemanie o pedagogicznych wartościach geometrii żywił Platon, sądząc, że kieruje ona uwagę ku temu, co wieczne i niezmienne. Stobajos przytacza następującą anegdotę:

Ktoś zaczął się uczyć u Euklidesa i kiedy poznał pierwsze twierdzenie, spytał:
– Co mi przyjdzie z tego, żem się tego nauczył?

Na to Euklides zawołał niewolnika i powiedział:

– Daj mu trzy obole, jeśli musi mieć zysk z tego, czego się uczy.

Omówimy bliżej główne linie rozumowania księgi I Elementów. Tekst poprzedzają 23 definicje, np. „Punkt jest tym, co nie ma żadnych części”, „Linia zaś jest długością bez szerokości”, „Równoległe są proste, które będąc na tej samej płaszczyźnie rozciągają się bez kresu w obie strony, ale w żadnej części się nie przetną” (przeł. M. Roszkowski). Linia prosta u Euklidesa jest zawsze skończona, tzn. jest odcinkiem wedle dzisiejszej terminologii. Dzisiejsi matematycy nie definiują wszystkich pojęć danej teorii, część z nich muszą bowiem stanowić pojęcia pierwotne, które przyjmuje się bez definicji, a ich sens ujawnia się dopiero, gdy badamy, w jaki sposób pojęcia występują one w aksjomatach i twierdzeniach.

Pięć postulatów głosi kolejno, że

1. Z każdego punktu do każdego innego można poprowadzić prostą (odcinek).
2. Odcinek można (obustronnie) przedłużać.
3. Z dowolnego środka można zakreślić okrąg przechodzący przez dany punkt.
4. Wszystkie kąty proste są wzajemnie równe.
5. Jeśli prosta przecina dwie inne proste, tworząca dwa kąty wewnętrzne mniejsze (w sumie) od dwóch kątów prostych, to można owe dwie proste przedłużyć tak, aby się przecięły.

Kąt prosty zdefiniowany jest tak, jak to widać na rysunku: gdy oba kąty utworzone przez półprostą o początku leżącym na danej prostej są równe, to kąty są kątami prostymi. Postulat 4 głosi, że dowolne kąty proste są równe, co znaczy tyle, że są przystające – mogą być na siebie nałożone tak, aby ich wierzchołki oraz ramiona się pokrywały (Euklides nie mówi tego wprost).

Pięć aksjomatów ogólnych stwierdza (w redakcji M. Kordosa):
1. Dwie wielkości równe trzeciej są równe.
2. Dodając do równych równe, dostajemy równe.
3. Odejmując od równych równe, dostajemy równe.
4. Wielkości dające się zamienić są równe.
5. Część jest mniejsza od całości.

Aksjomaty te stosowane są do porównania długości, kątów, figur, jak np. trójkąty. Mniejszy oznacza np. w przypadku odcinków, że po ich nałożeniu zostaje jeszcze jakaś niepokryta część większego (całości). Euklides nie posługuje się żadnymi miarami, porównuje tylko wielkości między sobą. Dlatego np. trójkąty są równe, gdy są przystające (można je na siebie nałożyć), ale także, gdy mają np. wspólną podstawę oraz jednakowe wysokości – dziś powiedzielibyśmy, że ich pola powierzchni są równe. Euklides nie myślał o długości jako liczbie, ani o polu prostokąta jako iloczynie długości boków, porównywał co najwyżej między sobą dwie wielkości.

Cały wykład podzielony jest na zagadnienia, które mogą być albo rozwiązaniem problemu konstrukcyjnego, albo twierdzeniem. W księdze I znajduje się 48 zagadnień, twierdzenie I,47 to twierdzenie dziś nazywane tw. Pitagorasa, I,48 to twierdzenie do niego odwrotne. Przyjrzyjmy się postępowaniu Euklidesa. Stosujemy dla przejrzystości nieco uwspółcześnioną terminologię, sformułowania nasze nie są wprawdzie dosłownym przekładem oryginału, ale też i nie odbiegają od niego zbyt daleko.

I,1 Mając dany odcinek AB, skonstruować na nim trójkąt równoboczny.

Konstrukcja sprowadza się do zakreślenia dwóch okręgów (Post. 3), które wyznaczą punkty przecięcia (co jednak nie wynika z aksjomatów Euklidesa, choć jest prawdą). Mając punkt przecięcia C, budujemy dwa odcinki AB oraz BC (Post. 1). Odcinki te są równe, ponieważ równe są odcinkowi AB (Aksj. 1). Trójkąt jest więc równoboczny. Warto zwrócić uwagę na eliminowanie kroków „oczywistych” i zastępowanie ich odwołaniami do postulatów i aksjomatów – w tym leży matematyczna siła Euklidesa, choć w oczach mniej matematycznie nastawionego czytelnika wywołuje to wrażenie (może nadmiernej) pedanterii.

I,2 Mając dany odcinek BC oraz punkt A nie leżący na nim, skonstruować odcinek AE=BC.

Łączymy w tym celu punkty AB (Post. 1) i budujemy trójkąt równoboczny za pomocą I,1. Promieniem BC zakreślamy okrąg o środku B (Post. 3). Przedłużamy następnie odcinek BD (Post. 2) do przecięcia z tym okręgiem H. Następnie promieniem HD zakreślamy okrąg o środku D. Przedłużenie AD (Post. 2) przetnie się z tym okręgiem w punkcie E. Odcinek AE (Post. 1) jest szukanym odcinkiem równym BC. Z aksjomatów ogólnych łatwo wnioskujemy, że odcinki te są równe, tzn. równe są ich długości (promień większego okręgu na rysunku to suma AB i boku trójkąta, odejmując potem bok trójkąta, otrzymujemy naszą tezę).
Warto zauważyć, że konstrukcje Euklidesa wykonywane są za pomocą linijki bez żadnej skali oraz cyrkla, który także nie pozwala przenosić odległości, lecz tylko poprwadzić okrąg z danego środka przez dany punkt (po przeniesieniu cyrkiel „nie pamięta” swego rozwarcia). Dzięki I,2 możemy uwolnić się od tego ograniczenia i odtwarzać odległość dwóch punktów w innym miejscu.

I,4 Dwa trójkąty, których dwa boki oraz zawarty między nimi kąt są równe, są przystające (równe).

Jest to cecha przystawania trójkątów bok-kąt-bok (bkb). Euklides dowodzi tego twierdzenia, nakładając na siebie oba trójkąty. Nie jest to postępowanie oczywiste, jeśli nie uważamy naszych figur za sztywne obiekty, które można przemieszczać bez zmiany kształtu i długości. David Hilbert przyjął w XIX w. to twierdzenie za jeden z aksjomatów w swoim wykładzie geometrii euklidesowej.

I,5 W trójkącie równoramiennym ABC, w którym AB=BC, kąty wewnętrzne przy podstawie są równe.

Przedłużamy ramiona trójkąta o jednakowe odcinki BF=CG. Trójkąty ABG i ACF są przystające na mocy poprzedniego twierdzenia, zatem także kąty ABG oraz ACF są równe. Trójkąty BFC i CGB są przystające na mocy tego samego twierdzenia (kąty BFC i BGC są równe, gdyż oba trójkąty pierwszej pary są przystające). Kąty ABC i BCA można przedstawić jako różnicę odpowiednio równych kątów (np. \sphericalangle ABC=\sphericalangle ABG-\sphericalangle CBG), muszą zatem być równe.
Twierdzenie to zyskało w średniowieczu nazwę Pons asinorum („ośli most”), nie wiadomo, czy z powodu kształtu towarzyszącego mu rysunku, czy też dlatego, że w tym miejscu ujawniał się już podział na tych, którzy rozumieją geometrię i na tych, którzy jej nie rozumieją. Pappus przedstawił prostszy dowód, w którym I,4 stosujemy do trójkątów BAC i CAB: ich boki są parami równe, a kąt przy wierzchołku jest tym samym kątem BAC, zatem oba trójkąty są przystające i kąty przy podstawie są równe. Euklides mógł mieć opory przeciwko takiemu potraktowaniu jednego trójkąta jako dwóch.

I,6 Jeśli kąty przy podstawie trójkąta są równe, to trójkąt jest równoramienny.

Euklides dowodzi tego twierdzenia przez sprowadzenie do niedorzeczności (reductio ad absurdum). Zakładamy, że teza twierdzenia jest fałszywa, a następnie staramy się wykazać, że wynika stąd zaprzeczenie założeń twierdzenia. Jeśli AB\neq AC, to któryś z odcinków jest większy, tzn. ma większą długość. Załóżmy, że AB>AC. Możemy wówczas na odcinku AB odłożyć odcinek AD=AC. Kąt DCB jest zatem mniejszy od kąta ACB. Jednocześnie trójkąt DBC jest równoboczny, a więc kąty DCB i DBC są równe na mocy poprzedniego twierdzenia. Kąt DBC jest tym samym, co kąt ABC, ergo ABC jest mniejszy od ACB wbrew założeniu.

I,9 Skonstruować dwusieczną danego kąta.

Na ramionach kąta odkładamy równe odcinki AD i AE. Następnie na odcinku AD konstruujemy trójkąt równoboczny. Jego trzeci wierzchołek wraz z wierzchołkiem kąta wyznaczają szukaną dwusieczną, co można łatwo udowodnić: kąty ADE i AED są równe jako kąty przy podstawie trójkąta równoramiennego. W takim razie także kąty ADF i AEF są równe i oba trójkąty ADF i AEF są przystające. Wobec tego kąty DAF i FAE są równe c.n.d.

I,11 Skonstruować prostopadłą do danej prostej w punkcie D.

Wyznaczamy na prostej dwa punkty A i B w równych odległościach od D: AD=DB. Następnie na odcinku AB konstruujemy trójkąt równoboczny. Jego trzeci wierzchołek C wraz z punktem D wyznaczają szukaną prostopadłą. Aby to udowodnić, zauważamy, że trójkąty ADC i BDC są przystające, a zatem kąty CDA i CDB są równe – spełniona jest więc definicja kąta prostego i oba te kąt są równe kątowi prostemu. Tym samym DC jest prostopadła do prostej AB.

I,20 (Nierówność trójkąta) Dwa boki trójkąta razem są dłuższe od trzeciego boku.

Niech będzie dany trójkąt CAB, chcemy dowieść, że odcinki AC wraz z CB są większe od AB. W tym celu na przedłużeniu AC odkładamy odcinek CD=CB. Kąt ABD jest większy od kąta CBD. Ten ostatni równy jest kątowi CDB, czyli ADB. W trójkącie ABD naprzeciwko większego kąta leży większy bok (I, 19; nie przytaczamy dowodu), a zatem AD=AC+CB>AB (stosując współczesny zapis).
Z twierdzenia tego wynika, że długość łamanej łączącej dwa punkty jest zawsze większa niż długość odcinka łączącego te punkty. W konsekwencji, jeśli połączymy oba punkty jakąś krzywą gładką, ale taką że zarówno samą krzywą, jak i jej długość można dowolnie przybliżać za pomocą łamanych, to długość łuku krzywej nie może być mniejsza niż długość odcinka łączącego dane punkty. Inaczej mówiąc, odcinek jest krzywą o najmniejszej długości (przy ustalonych obu końcach). Euklides nie dowodzi takiego twierdzenia, ale było ono znane greckim geometrom.
Dopiero blisko połowy księgi I staje się potrzebny Postulat 5.

I,29 Jeśli prosta EF przecina parę prostych równoległych AB i CD, to kąty naprzemianległe wewnętrzne są równe.

Wykażemy, że kąt AGF równy jest kątowi EHD. Załóżmy, że oba te kąty nie są równe. Niech np. AGF będzie większy od EHD. Ponieważ kąty AGF i BGF dopełniają się do dwóch kątów prostych (I,14; nie przytaczamy dowodu), więc suma kątów BGF i EHD jest mniejsza od dwóch kątów prostych. Z Post. 5 wynika, że proste AB i CD (po ewentualnym przedłużeniu) przetną się, nie są zatem – wbrew założeniu – prostymi równoległymi.
Postulat 5 sformułowany został tak, aby wygodnie się nim było posługiwać do wykazania, że dwie proste nie są równoległe. Nie wydawał się on tak oczywisty jak pozostałe i wzbudzał zawsze rozmaite wątpliwości. Jest on równoważny innemu postulatowi sformułowanemu przez Playfaira: Przez punkt nie leżący na danej prostej można przeprowadzić dokładnie jedną prostą równoległą do danej. Postulat 5 jest także równoważny twierdzeniu o sumie kątów wewnętrznych trójkąta.

I,32 Suma kątów wewnętrznych trójkąta równa jest dwóm kątom prostym.

Wystarczy zauważyć równość zaznaczonych kątów na rysunku (linia przerywana jest równoległa do boku trójkąta).

I,47 (Tw. Pitagorasa) W trójkącie prostokątnym suma kwadratów zbudowanych na przyprostokątnych jest równa kwadratowi zbudowanemu na przeciwprostokątnej.

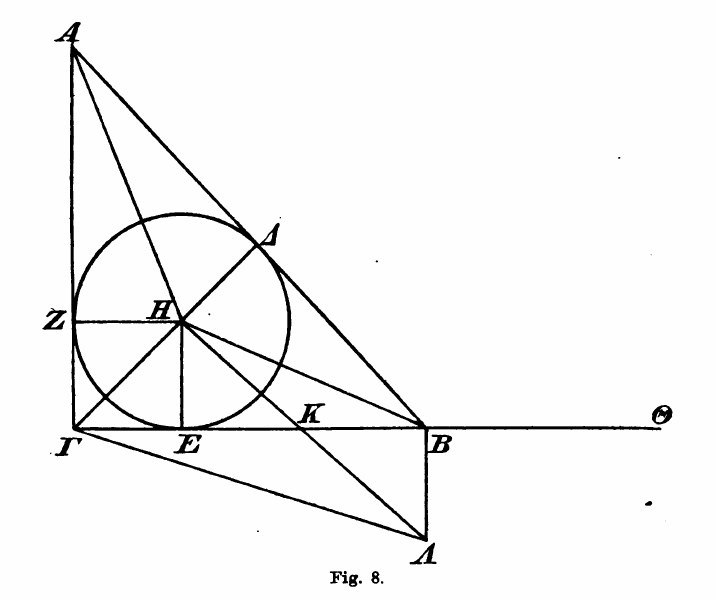
Zwróćmy uwagę na sformułowanie: należy najpierw skonstruować kwadraty, o których mowa w twierdzeniu, a następnie wykazać, że suma (pól) dwóch mniejszych kwadratów jest równa polu kwadratu największego. Wysokość trójkąta opuszczona z kąta prostego po przedłużeniu dzieli kwadrat na dwa prostokąty. Euklides wykazuje, że dla trójkąta ABΓ oba pola zaznaczone na zielono oraz oba pola zaznaczone na niebiesko są równe.

Dowód Euklidesa korzysta z konstrukcji I,46 kwadratu na danym odcinku oraz linii równoległej do BΔ i ΓE przechodzącej przez dany punkt A (I,31). Wykazuje następnie, że AH jest przedłużeniem AΓ oraz AΘ jest przedłużeniem AB (I,14). Trójkąty ABΔ oraz ZBΓ są przystające na mocy twierdzenia I,4 (bkb). Prostokąt BΛ o podstawie BΔ ma tę samą wysokość co trójkąt ABΔ o tej samej podstawie. Na mocy I,41 prostokąt jest dwa razy większy od trójkąta (to wynik równoważny wzorowi na pole trójkąta, gdy określimy pole prostokąta). Kwadrat BH jest z tego samego powodu dwa razy większy od trójkąta ZBΓ o podstawie ZB. W analogiczny sposób pokazać można, że oba pola zaznaczone na niebiesko są równe, co kończy dowód.

W księdze VI Euklides przytacza inny dowód tw. Pitagorasa, oparty na podobieństwie mniejszych trójkątów na rysunku i trójkąta wyjściowego. Ten drugi dowód znany był prawdopodobnie wcześniej, dowód I,47, pochodzący zapewne od samego Euklidesa, jest bardziej zadowalający matematycznie, gdyż używa mniejszej liczby założeń: w księdze I daleko jeszcze jesteśmy od tak subtelnych konstrukcji jak figury podobne.
Ostatnie twierdzenie tej księgi I,48 jest odwrotne do tw. Pitagorasa: Jeśli spełniony jest warunek pól dla kwadratów zbudowanych na bokach trójkąta, to trójkąt ów jest prostokątny.

Elementy są podręcznikiem i były nim już w chwili powstania. Ścisłość rozumowań Euklidesa stała się wzorem dla przyszłych matematyków. Wybitny matematyk XX wieku André Weil pisał: „ [Elementy] Euklidesa to pierwszy zachowany tekst matematyczny, w którym pojęcie dowodu utożsamione zostało z łańcuchem wnioskowań pozbawionym luk; nie bez powodu ten sposób widzenia przedmiotu zachował swą aktualność do dziś”.

Nie sposób oczywiście przedstawić nawet pobieżnie wpływu książki czytanej w ciągu dwudziestu kilku wieków przez tysiące ludzi: wybitnych matematyków, jak i myślicieli czy po prostu uważnych czytelników mniej lub bardziej oddalonych od nauk ścisłych.

Greckie manuskrypty Elementów przechowywane były w Bizancjum. Od nich pochodziły przekłady arabskie, które z kolei dały początek rozpowszechnianiu się tekstu zarówno na Wschód (języki hebrajski, syryjski, perski), jak i na Zachód (łacina). W europejskim średniowieczu przekładano Euklidesa z arabskiego na łacinę wielokrotnie w wieku dwunastym i później. Już sama międzynarodowa lista tłumaczy daje pojęcie o zainteresowaniu Elementami: Adelard z Bath, Hermann z Karyntii, Gerard z Cremony, Robert z Chester, Campanus z Novary. Przekład tego ostatniego stał się podstawą pierwszego drukowanego wydania Elementów w Wenecji w roku 1482. W XVI wieku udało się też dotrzeć do tekstu greckiego (w wersji Teona). Od tamtej pory ukazały się niezliczone wydania oraz przekłady na języki narodowe (brak nadal kompletnego przekładu polskiego, choć już w 1808 Józef Czech, dyrektor Liceum Krzemienieckiego, przełożył osiem ksiąg, opierając się na angielskiej wersji Roberta Simonsa).

Twierdzenie Pitagorasa w weneckim wydaniu z 1482 r. (numeracja twierdzenia lekko w nim szwankowała)

Geometria oraz arytmetyka miały w średniowieczu mocną pozycję jako sztuki wyzwolone wchodzące w skład quadrivium („czterodroże”) wraz z astronomią i muzyką (która obejmowała głównie teoretyczną naukę o proporcjach dźwięków w różnych skalach). Także i później podstawy geometrii stanowiły nieodzowny element wykształcenia, Elementów długo jeszcze używano jako podręcznika. Bertrand Russell, logik i filozof, wspomina: „W wieku jedenastu lat zacząłem Euklidesa z moim bratem w roli tutora. Było to w moim życiu wielkie wydarzenie, równie olśniewające co pierwsza miłość. Wcześniej nie wyobrażałem sobie nawet, że istnieje na świecie coś tak zachwycającego. Kiedy przeszedłem Zagadnienie 5 (Pons asinorum), brat powiedział mi, że powszechnie uchodzi ono za trudne, ja jednak nie napotkałem w nim żadnych trudności. To wtedy po raz pierwszy zaświtało w mej głowie, że może obdarzony zostałem jakąś inteligencją”. Kilka lat młodszy Albert Einstein nie uczył się wprawdzie z Elementów, lecz z podręcznika będącego ich zmodernizowaną wersją; także dla niego odkrycie geometrii było wielkim przeżyciem, wspominał potem podręcznik jako „świętą książeczkę”, co w jego ustach – uduchowionego niedowiarka i spinozisty – miało swoją wymowę. Einstein sądził wręcz, że głęboki wstrząs intelektualny, jaki wówczas przeżył, stanowi niejako rodzaj probierza, czy ktoś się do nauki nadaje, czy nie. Zanim jeszcze podręcznik trafił w jego ręce, udało mu się znaleźć dowód twierdzenia Pitagorasa oparty na podobieństwie trójkątów (VI,31).

Metoda geometryczna kusiła też filozofów. Thomas Hobbes, mając już czterdzieści lat, natknął się w bibliotece znajomego gentlemana na egzemplarz Elementów, które otwarte były na stronie zawierającej twierdzenie Pitagorasa. Przeczytawszy jego treść, wykrzyknął: na Boga, to niemożliwe! Potem jednak cofając się stopniowo do twierdzeń, na których oparty był dowód, zrozumiał, że rozumowanie Euklidesa jest bez zarzutu. René Descartes sam był wybitnym matematykiem i z geometrią zapoznał się wcześnie w jezuickim kolegium w La Flèche. Właśnie na goemetrii wzorował się w swym podejściu do filozofii, która miała być nowym początkiem ludzkiej wiedzy. „Owe długie łańcuchy uzasadnień, zupełnie proste i łatwe, którymi zazwyczaj posługują się geometrzy, by dotrzeć do swych najtrudniejszych dowodzeń, dały mi sposobność do wyobrażenia sobie, że wszystkie rzeczy dostępne poznaniu ludzkiemu wynikają w taki sam sposób wzajemnie ze siebie, a także, że nie mogą istnieć tak odległe, do których byśmy wreszcie nie dotarli, i tak ukryte, których byśmy nie wykryli, bylebyśmy tylko nie przyjmowali za prawdziwą żadnej rzeczy, która by prawdziwą nie była, i zachowywali zawsze należyty porządek w wyprowadzaniu jednych z drugich” (przeł. W. Wojciechowska, Rozprawa o metodzie, PWN 1981, s. 23). Zdaniem Immanuela Kanta przedmioty, które bada matematyka: przestrzeń i czas nie pochodzą z doświadczenia, ale mają swe źródło w poznającym przedmiocie. Geometria stała się w ten sposób nauką o jedynie możliwej przestrzeni.

Tymczasem matematycy nabierali coraz więcej wątpliwości. Karl Friedrich Gauss już w roku 1813 rozmyślał nad geometrią nieuklidesową, lecz oportunistycznie nie zdecydował się na publikację swych wyników. Także Ferdinand Karl Schweikart, profesor prawa, rozwijał podobne idee w zaciszu gabinetu. Dopiero János Bolyai i Nikołaj Iwanowicz Łobaczewski, niezależnie od siebie zaryzykowali publikację prac sprzecznych z dotychczasową tradycją, nie były one przyjęte dobrze. Obaj zajmowali się geometrią hiperboliczną, w której istnieje nieskończenie wiele prostych równoległych do danej prostej. Postulat 5 Euklidesa jest bowiem niezależny od pozostałych i równie dobrze można zbudować konsekwentną geometrię, wychodząc z jego zaprzeczenia. Pod koniec XIX wieku David Hilbert podał ścisłe sformułowanie geometrii euklidesowej. Znalazło się w nim dwadzieścia aksjomatów, trzy pojęcia pierwotne (punkt, linia prosta, płaszczyzna) oraz cztery relacje pierwotne (leżenia pomiedzy, zawierania oraz przystawania odcinków oraz kątów). Różnica w podejściu między dawną geometrią a jej nowoczesnym, abstrakcyjnym sformułowaniem podkreślona została przez Hilberta następująco: „Powinno się w każdej chwili móc wstawić w miejsce punktów, linii i płaszczyzn – stoły, krzesła i kufle do piwa” (oczywiście pod warunkiem, że obiekty te spełniają aksjomaty geometrii).

Pitagoras i Vincenzo Galilei: początek i koniec tradycji pitagorejskiej (VI w. p.n.e., 1588)

Pitagoras pierwszy nazwał się filozofem, lecz stał się założycielem sekty na poły religijnej, która przekazywała sobie wierzenia, obyczaje, obrządki i nie dopuszczała nikogo bez długiego procesu formowania charakteru i umysłu. Pitagorejczycy wierzyli w wędrówkę dusz, obejmującą także dusze zwierzęce, więc nie składali ofiar ze zwierząt i starali się nie jeść mięsa, zazwyczaj zadowalali się warzywami, kaszą i przyprawami. Mieli też osobliwą na tle ówczesnej Grecji koncepcję piękna:

Piękny jest więc widok całego nieba i poruszających się po nim gwiazd, jeśli ktoś potrafi dostrzec ich porządek; a piękne jest to wszystko przez uczestniczenie w tym, co pierwsze i dostrzegalne umysłem. Pierwsza zaś jest dla Pitagorasa natura liczb i stosunków liczbowych, ogarniająca całość rzeczywistości, zgodnie z nimi bowiem wszechświat jest mądrze zbudowany i prawidłowo uporządkowany; mądrość zaś jest wiedzą o tym, co piękne i pierwsze, boskie i niezniszczalne, zawsze takie samo i podlegające takiemu samemu porządkowi (…) filozofia natomiast to umiłowanie takiej kontemplacji [Jamblich, O życiu pitagorejskim, przeł. J. Gajda-Krynicka].

Wszechświat postrzegali pitagorejczycy jako κόσμος – kosmos, czyli pięknie złożoną harmonijną całość. Pitagoras odkrył, że prostym proporcjom liczbowym, takim jak 2:1; 3:2 oraz 4:3 odpowiadają harmonijnie współbrzmiące interwały dźwięków: oktawa, kwinta i kwarta. Fakt ten stał się punktem wyjścia całej jego filozofii i kosmologii. Odgrywały w nich rolę muzyka i matematyka, ich związek był fundamentalny. Muzyka miała bowiem swe odbicie w strukturze wszechświata, nie była jedynie sztuką wydawania sugestywnych dźwięków. W ten sposób, po raz pierwszy, wszechświat stał się matematyczny.

Pitagorejczycy uzasadniali owe proporcje dźwięków w sposób numerologiczny. Ich zdaniem liczby 1, 2, 3, 4, były wieloznacznymi symbolami. Suma tych czterech liczb nazywana była tetraktys – arcyczwórką. Arytmetyka miała być także podstawą geometrii: przestrzeń wyobrażali sobie pitagorejczycy jako „skwantowaną”, złożoną z dyskretnych wielkości. Doprowadziło to do kryzysu: zgodnie bowiem z twierdzeniem Pitagorasa długość przekątnej kwadratu o boku równym 1 wynosi . Jeśli przyjąć, że można tę liczbę zapisać jako stosunek liczb całkowitych (jak powinno być w dyskretnej przestrzeni), dochodzi się do sprzeczności. Dziś mówimy, że  jest liczbą niewymierną. Odkrycie tego faktu wstrząsnęło pitagorejczykami.

Wróćmy jednak do harmonii dźwięków. Mamy tu początek fizyki matematycznej – oto pewne stosunki w przyrodzie poddane są zasadom matematyki. Z czasem miało się okazać, że jest to prawda w odniesieniu do całej przyrody, choć uznanie tego faktu zajęło ludzkości ponad dwa tysiące lat. Dziś nie mamy wątpliwości co do nadzwyczajnej skuteczności matematyki w badaniu przyrody. Niektórzy uważają nawet, że w każdej nauce tyle jest prawdy, ile jest w niej matematyki.

W jakim sensie proporcje związane są z parami dźwięków?

Jamblich tak pisze o okolicznościach dokonania owego odkrycia przez Pitagorasa:

Rozmyślał kiedyś i zastanawiał się, czy da się wymyślić dla słuchu jakieś pomocnicze narzędzie, pewne i nieomylne, jakie ma wzrok w cyrklu, w miarce (…), dotyk zaś w wadze i w wynalazku miar; a przechadzając się w pobliżu warsztatu kowalskiego, jakimś boskim zrządzeniem losu usłyszał młoty kujące żelazo na kowadle i wydające dźwięki zgodne ze sobą, z wyjątkiem jednej kombinacji. Rozpoznał zaś w nich współbrzmienie oktawy, kwinty i kwarty. Dostrzegł natomiast, że dźwięk pośredni między oktawą a kwintą sam w sobie pozbawiony jest harmonii, lecz uzupełnia to, czego w innych jest w nadmiarze. Zadowolony zatem, ponieważ została mu zesłana pomoc od boga, poszedł do warsztatu i po wielu rozmaitych próbach odkrył, iż różnica dźwięków rodzi się z ciężaru młotów, nie z siły uderzających, nie z kształtu narzędzi ani też nie z przekształceń kutego żelaza; a zbadawszy dokładnie odpowiednie wagi i ciężary młotów, poszedł do domu i wbił między ściany, od kąta do kąta, jeden kołek, jeden by z wielości kołków albo też z różnej ich natury nie zrodziła się jakaś różnica; następnie przywiesił do kołka w równym od siebie oddaleniu cztery struny z jednakowej materii, jednakowej długości, grubości i jednakowo sporządzone, przywiązawszy do każdej z dołu ciężar i wyrównawszy całkowicie długość strun. Następnie uderzając jednocześnie w dwie struny na przemian, odnalazł wymienione wyżej współbrzmienia, inne w każdym ze związków. Odkrył bowiem, że ta, która obciążona była największym ciężarem wraz z tą, która miała ciężar najmniejszy, razem uderzone tworzą stosunek oktawy. Jedna bowiem miała dwanaście ciężarków, druga zaś sześć; w podwójnej proporcji ujawniła się oktawa, jak to wskazywały same ciężarki. [przeł. J. Gajda-Krynicka]

Jamblich był syryjskim pitagorejczykiem żyjącym w III/IV w. n.e., a więc niemal tysiąc lat po filozofie z Samos. Dlatego, jak to się zdarza zwolennikom bardziej entuzjastycznym niż rozumiejącym, poplątał to i owo w tej historii. Wiemy, że pragnął swymi opowieściami przewyższyć zdobywające sobie popularność historie o innym mistrzu, Jezusie Chrystusie.

Jamblich przedstawia nam etapy odkrycia: mamy więc problem (jak proporcje mogą być odwzorowane dźwiękami?), iluminację pod wpływem przypadkowego bodźca (młoty kowalskie), analizę i wyjaśnienie sensu owej iluminacji, a następnie przeprowadzenie eksperymentu, w którym początkowa sytuacja zostaje sprowadzona do najważniejszej istotnej zależności: chodzi nie młoty, lecz dźwięki; można je badać za pomocą jednakowych strun pod działaniem różnych sił naciągu.

Mamy właściwie przepis, jak należy odkrywać matematyczne prawa przyrody, oczywiście w stosownej chwili musimy otrzymać pomoc od boga, inaczej wkroczymy w jedną z tych niezliczonych ścieżek, które nigdy nie zawiodły do żadnego rozsądnego punktu. Bywa i tak, że ciąg dalszy odnajduje się po wielu latach – w tym sensie z oceną wartości pewnych prac naukowych należy poczekać.

Niestety, ciąg dalszy opowieści Jamblicha dowodzi, że nie zrozumiał on odkrycia mistrza. Nie chodzi bowiem o siły naciągu, lecz długości strun. To one muszą być w odpowiedniej proporcji. Np. kwintę otrzymamy, biorąc taką samą strunę z takim samym naciągiem, lecz o długości krótszej w proporcji 2:3. Przez wieki powtarzano błąd Jamblicha, nie zadając sobie trudu mierzenia czegokolwiek. Powszechnie sądzono, że owe proporcje zawarte są we wszystkich sposobach wydobywania dźwięków tak, jak to widzimy na ilustracji poniżej, pochodzącej z przełomu XV i XVI wieku.

W XVI wieku powiększono listę dźwięków współbrzmiących harmonijnie, uzasadniając to zresztą także na sposób pitagorejski. Gioseffo Zarlino, maestro di capella San Marco w Wenecji, proponował dołączenie 5 i 6 do starożytnego zestawu. Uzasadniał to rozmaitymi „nadzwyczajnymi” własnościami liczby sześć: jest liczbą doskonałą (równą sumie swych podzielników), sześć było dni Stworzenia itd.

Empiryczne podejście do tego zagadnienia zawdzięczamy sceptycyzmowi i jadowitemu charakterowi Vincenza Galilei, muzyka i teoretyka muzyki z Florencji. Był on uczniem Zarlina, lecz zaatakował go bezpardonowo w wydanym w roku 1589 traktacie. Uważał wszelką numerologię za nonsens i postanowił wykazać to doświadczalnie. Stosunki dźwięków nie są bowiem związane jednoznacznie ze stosunkami liczbowymi. Np. kwintę możemy uzyskać nie tylko skracając strunę w stosunku , ale także zwiększając siłę naciągu w proporcji . Mamy więc następujące prawo: chcąc otrzymać dany wyższy dźwięk możemy albo skrócić strunę razy, albo zwiększyć siłę naciągu razy. Było to pierwsze w ogóle nowożytne prawo fizyki matematycznej.
W ten sposób numerologia została pogrążona, gdyż widzimy, że równie dobrze można by wiązać kwintę z proporcją . Był to tylko jeden z wielu argumentów wysuwanych w traktacie przeciwko Zarlinowi. Vincenzo Galilei miał zdolnego syna o imieniu Galileo, któremu przekazał swój choleryczny temperament i namiętną pogardę dla umysłowej niższości. Niewykluczone, że eksperymenty nad tą kwestią prowadzili zresztą obaj razem, zapewne w roku 1588. W roku następnym Galileo uzyskał skromną posadę na uniwersytecie w Pizie. Napisał tam poemat na temat noszenia togi, w którym drwił z księży (wrogowie wszelkiej niewygody), uczonych kolegów (są jak flaszki wina: nieraz we wspaniale oplecionych butelkach zamiast bukietu czuje się wiatr albo perfumowaną wodę i nadają się tylko do tego, by do nich nasikać), a także twierdził, że chodzenie nago jest największym dobrem. Zajął się też poważnie mechaniką. Możliwe, że to ciężarki zawieszone na końcu struny w eksperymentach prowadzonych z ojcem, a nie kandelabr w katedrze, nasunęły mu myśl o wahadle.

Prawo odkryte przez Vincenza Galileo łatwo uzasadnić. Prędkość rozchodzenia się dźwięku w strunie naciągniętej siłą która ma gęstość liniową (masa na jednostkę długości)  równa się

Jeśli końce struny są nieruchome, to długość powstającej fali jest dwa razy większa niż długość struny : . Zatem częstość drgań struny jest równa

Napięcie struny wchodzi więc w potędze , stąd wynik Vinzenza Galileo.

Einstein o Lukrecjuszu, 1924

PIOTR: Ktoś ty? DUCH: Lukrecy, Lewiatan, Voltaire, Alter Fritz, Legio sum.

[A. Mickiewicz, Dziady]

Dziś zajmiemy się diabłem zwanym przez wieszcza Lukrecy, czyli Lukrecjusz.

Żyjący w I w. p.n.e. Titus Lucretius Carus, autor poematu O rzeczywistości (in. O naturze rzeczy), był zarazem wybitnym poetą i zwolennikiem atomizmu w wersji Epikura. Idea, że świat zbudowany jest z atomów i nie jest kierowany przez osobowe bóstwa, przyjmowała się trudno i z oporami. Człowiek ma umysł, który chętnie postrzega rzeczywistość w kategoriach celu. Dlatego w różnych epokach od starożytności począwszy traktowano poglądy Lukrecjusza jako absurdalne i heretyckie. Nie wierzono, aby jako tako uładzony wszechświat mógł powstać bez czynnej interwencji bóstwa. Zderzające się w nieskończoności atomy wydawały się wizją jałową i ponurą, a do tego wielce nieprawdopodobną: no bo jak długo musiałyby się zderzać atomy, by utworzyć Einsteina? Wiemy jednak, że Einstein powstał nie z mgławicy gazowej, lecz jako człowiek, a człowiek od australopiteka itd. itp. Życie na Ziemi powstało (w skali kosmicznej) niemal nazajutrz po utworzeniu się planety, co wskazywałoby albo na to, że ewolucja od chemii do biologii nie jest aż tak nieprawdopodobna, albo wracamy do kapłanów i ich wyjaśnień na ten temat, które nic nie wyjaśniają.

Poniższy tekst jest wstępem Alberta Einsteina do poematu Lukrecjusza. Uczony zdobył w tym czasie światową sławę, choć nie wszystkich Niemców to cieszyło, albowiem był on Żydem. W kraju, po puczu monachijskim Adolfa Hitlera i wciąż w kryzysie gospodarczym, narastały kompleksy i nacjonalizm. Toteż Einstein czuł się tam, jak „ktoś, kto leży w dobrym łóżku, lecz oblazły go pluskwy”. Znamy to uczucie.

https://kierul.wordpress.com/2013/02/01/einstein-zydowski-prorok-we-wlasnym-kraju/

https://kierul.wordpress.com/2012/11/22/einstein-i-mann-koniec-wielkich-niemiec/

Każdy, kto nie idzie całkowicie z duchem naszego czasu i kto czuje się niekiedy obserwatorem otaczającego świata, a zwłaszcza duchowej postawy swych współczesnych, nie może pozostać obojętny na czar dzieła Lukrecjusza. Widzimy w nim bowiem, jak wyobraża sobie świat człowiek niezależny, wyposażony w żywe doznania zmysłowe i zdolność rozumowania, obdarzony naukową i spekulatywną ciekawością, człowiek, niemający najmniejszego pojęcia o osiągnięciach współczesnej nauki, które nam wpojono w dzieciństwie, nim jeszcze mogliśmy się z nimi skonfrontować w sposób świadomy i krytyczny.

Głębokie wrażenie robi na nas niezmącona pewność Lukrecjusza – wiernego ucznia Demokryta i Epikura – że świat jest zrozumiały, tzn. wszystko, co się w nim dzieje, powiązane jest łańcuchem przyczyn i skutków. Żywi on mocne przekonanie, a nawet sądzi, iż potrafi udowodnić, że wszystko bierze się z poddanego prawom ruchu niezmiennych atomów, którym nie przypisuje żadnych innych własności prócz geometrycznych i mechanicznych. Jakości zmysłowe, takie jak ciepło, zimno, barwa, zapach i smak, sprowadzają się do ruchu atomów; to samo dotyczy życia. Dusza i umysł są w jego mniemaniu zbudowane ze szczególnie lekkich atomów, wiąże on przy tym (niezbyt konsekwentnie) pewne szczególne własności materii z konkretnymi cechami doświadczenia.

Za najważniejszy cel swego dzieła uważa Lukrecjusz uwolnienie człowieka od niewolniczego strachu, wynikłego z religii i przesądów, a podsycanego i wykorzystywanego przez kapłanów dla własnych celów. Z pewnością jest to dla niego bardzo ważne. Wydaje się jednak, że powoduje nim przede wszystkim chęć przekonania czytelników do atomistyczno-mechanistycznego obrazu świata, choć nie odważa się tego powiedzieć wprost praktycznie nastawionym Rzymianom. Wzruszający jest też jego szacunek dla Epikura oraz języka i kultury Grecji, które uważa za znacznie doskonalsze niż język łaciński i kultura rzymska. Przynosi Rzymianom zaszczyt, że można było mówić im takie rzeczy. Czy któryś ze współczesnych narodów potrafiłby wypowiadać się tak szlachetnie o innym?

Wiersze Dielsa czyta się tak naturalnie, iż zapomina się, że to przekład.

Berlin, czerwiec 1924 roku

http://einsteinpapers.press.princeton.edu/vol14-doc/498

Jak Ptolemeusz nie odkrył prawa Snella

Klaudiusz Ptolemeusz był astronomem i astrologiem, wierzył zapewne w boskość ciał niebieskich i studiowanie ich ruchów traktował jako udział w pewnym misterium. Bo też zrozumienie każdej, nawet drobnej tajemnicy świata ma w sobie coś z misterium i z obrzędu wtajemniczenia. Nie trzeba do tego mieszać ludzi w szatach rytualnych, profesjonalistów, którzy zazwyczaj niczego nie rozumieją. Nie potrzeba pleść o Bogu, o którym wszyscy wiemy bardzo niewiele.

Wyjaśnienie ruchu planet musiało Ptolemeuszowi przynieść wielką satysfakcję: dokończył dzieła wielu pokoleń. My dzisiaj patrzymy na jego teorię jak na wstęp do Kopernika i Keplera, lecz przez czternaście wieków uważano ją za niedościgniony wzór. Geocentryzm nikomu właściwie nie przeszkadzał, był oczywisty, tak jak my uważamy za oczywistość, że Ziemia się porusza, choć nie każdy potrafiłby wskazać doświadczalne dowody tego faktu. Ptolemeusz zresztą doskonale sobie zdawał sprawę z możliwości ruchu Ziemi, odrzucał ją przedstawiając pewne argumenty, a więc nie z braku wyobraźni.

Był zawodowym uczonym, zajmował się całością nauk matematycznych, a więc także geografią i skalami muzycznymi oraz optyką. Pierwszy opisał ilościowo i doświadczalnie zbadał zjawisko załamania światła. Używał do tego następującego przyrządu.

Światło biegnie po łamanej ZEH, DEB jest linią rozdziału dwóch ośrodków, np. na dole mamy wodę albo szkło (w kształcie połowy walca), a u góry powietrze. Koło zaopatrzone jest w podziałkę w stopniach. Uczony mierzył kąty padania oraz załamania . Oto jego wyniki dla granicy powietrze-woda.

 

i	r
10	8
20	15,5
30	22,5
40	29
50	35
60	40,5
70	45,5
80	50

Jest to rzadki przypadek starożytnej pracy eksperymentalnej poza astronomią. Optyka była przedłużeniem astronomii, więc dość naturalne było zainteresowanie zjawiskami świetlnymi. Tabelka Ptolemeusza nie jest jednak do końca wynikiem doświadczalnym, zauważymy to, analizując dokładniej wartości kątów załamania i ich różnice.

i	r	pierwsze różnice	drugie różnice
10	8	8
20	15,5	7,5	-0,5
30	22,5	7	-0,5
40	29	6,5	-0,5
50	35	6	-0,5
60	40,5	5,5	-0,5
70	45,5	5	-0,5
80	50	4,5	-0,5

Uczony najwyraźniej „poprawiał” surowe dane eksperymentalne, być może nawet nie wykonał wszystkich pomiarów, zachował się jak niesumienny student podczas zajęć laboratoryjnych: i tak przecież wiadomo, co ma wyjść. Nie należy z tego powodu wszczynać larum, że przyłapaliśmy Ptolemeusza na oszustwie: w jego czasach i jeszcze bardzo długo potem starano się raczej uzyskać pewną formułę, jakiś rodzaj matematycznego zrozumienia zamiast relacjonować listę wyników obarczonych błędami. Teoria i eksperyment spotykały się w nieco innym miejscu niż dziś. Ptolemeusz zapewne chciał po inżyniersku rozumieć, skąd się biorą liczby w jego tabelce. Funkcja liniowa tu nie pasuje, bo wówczas różnice byłyby stałe. Jeśli drugie różnice (czyli różnice kolejnych różnic) są stałe, to znaczy, że opisujemy obserwowaną zależność funkcją kwadratową (*). Jej wykresem będzie parabola.

Czerwone kropki są prawidłowymi wynikami dla kątów załamania w wodzie. Błędy nie są wielkie, choć znacznie przewyższają niedokładności tolerowane wówczas w astronomii. Podobne dane przedstawia Ptolemeusz dla szkła, także i one są dopasowane do paraboli.

W istocie Ptolemeusz stracił okazję do odkrycia prawa bardziej zadowalającego pod względem matematycznym. Podał on bowiem także wyniki dla załamania z wody do szkła. Także i tym razem dopasował je do funkcji kwadratowej, choć z pewnymi anomaliami. Nie zauważył jednak, że skoro ma dane dla granic ośrodków powietrze-woda oraz szkło-woda, to kąty dla załamania z wody do szkła powinny już wynikać z poprzednich danych. Wystarczy bowiem wyobrazić sobie następującą sekwencję ośrodków: woda-powietrze-szkło. Dla obu granic znamy zależności miedzy kątami po obu stronach (Ptolemeusz wiedział, że kierunek biegu promieni nie ma znaczenia w załamaniu, wyobrażał sobie zresztą nie promienie świetlne, lecz promienie wzrokowe, które wybiegają z oka). Możemy sobie następnie wyobrazić, że warstwa powietrza staje się coraz cieńsza: kąty w wodzie i w szkle cały czas są takie same, logicznie jest więc przypuścić, że pierwsze dwie zależności dają nam tę trzecią (woda-szkło). Ptolemeusz nie poszedł tą drogą i chyba nie zauważył, że przybliżenie kwadratowe jest nie do utrzymania dla trzeciej pary ośrodków. W gruncie rzeczy prawo Snella, choć takie proste, wymaga spojrzenia na zjawisko załamania w odpowiedni sposób, mieści w sobie od razu pewną teorię. Nie miejmy za złe Ptolemeuszowi w II w.n.e., że nie poradził sobie z problemem, który jeszcze na początku wieku XVII okazał się za trudny dla samego Johannesa Keplera. Ostatecznie prawo załamania odkrył Ibn Sahl, żyjący w X wieku, kiedy nasi przodkowie kryli się po lasach, a w XVII wieku niezależnie od siebie Thomas Harriot, Willebrord Snell i René Descartes. Tylko ten trzeci opublikował to prawo, a także jego mechaniczne uzasadnienie, zresztą fałszywe.

(*) Łatwo zauważyć, że różnice dla funkcji kwadratowej są liniową funkcją argumentu. W przypadku biegu promieni z powietrza do wody Ptolemeusz stosuje (niejawnie) funkcję

Funkcja odwrotna nie jest już kwadratowa (musimy rozwiązać ostatnią równość względem ). Zatem złożenie tej funkcji odwrotnej z funkcją kwadratową nie może nam dać funkcji kwadratowej dla trzeciej pary ośrodków.

Dane Ptolemeusza

 

Wzór Herona, Archimedes i zasada Arnolda

Heron z Aleksandrii żył gdzieś między datą śmierci Archimedesa (212 p.n.e.) a Pappusem, żyjącym w IV w.n.e. Jedyna informacja pozwalająca lepiej zlokalizować go w czasie, to zaćmienie Księżyca w roku 62 n.e., które opisał. Prawdopodobnie więc w owym roku zaliczał się między żywych, nim – jak wszyscy – przeszedł do krainy cieni. Nauczał w aleksandryjskim Muzeum (które było czymś w rodzaju elitarnej uczelni i instytutu badawczego), pozostawił wiele dzieł, i to one nas tu interesują.

Nastawiony praktycznie, w swej Pneumatyce opisał wiele urządzeń poruszanych siłą powietrza albo pary wodnej. Były tam urządzenia takie, jak wrota świątynne, które same się otwierały, gdy rozpalono ogień na ołtarzu. Trzeba było zaczekać, aż w naczyniu z prawej skondensuje się dostatecznie dużo pary, czas biegł wtedy wolniej, ludzie się nie spieszyli.

Samoczynne urządzenia zaspokajały potrzebę cudowności i podziwu, tę samą co dziś Gwiezdne wojny albo krwawiąca hostia w Legnicy, poza tym jednak nie służyły do niczego. Heron napisał podręcznik efektów specjalnych.

Zawartość [tego dzieła] stanowiła zawsze źródło konsternacji i rozpaczy dla poważnie myślących badaczy. Heron opisuje wprawdzie pewne użyteczne urządzenia, jak pompa strażacka albo organy wodne, ale cała reszta to zabawki, mechaniczne kukiełki albo przyrządy do salonowych sztuczek magicznych. Naczynia, które tryskają wodą bądź winem oddzielnie albo w stałych proporcjach, śpiewające ptaszki i grające trąbki, figurki poruszające się, gdy na ołtarzu rozpali się ogień, zwierzęta, które piją, gdy poda im się wodę – jak szanować autora, który poważnie zajmuje się tymi wszystkimi błahostkami? (A.G. Drachmann)

Napisał też Heron sporo dzieł geometrycznych, ale nastawionych inżyniersko, praktycznych. W jednym z nich, Metrikon, znajdują się metody obliczania pola powierzchni oraz objętości brył. W Egipcie, gdzie po każdym wylewie Nilu trzeba było od nowa wyznaczać granice działek rolnych, geometria praktyczna była w cenie. Geometria po grecku znaczy właśnie sztukę mierzenia ziemi.

Oto jeden z przykładów Herona. Mamy trójkąt o bokach 7, 8, 9. Znaleźć jego pole. Uczony podaje przepis: obliczamy najpierw długość obwodu i dzielimy ją przez dwa:

Następnie od liczby tej odejmujemy długości poszczególnych boków :

Uzyskane w ten sposób cztery liczby mnożymy przez siebie i wyciągamy pierwiastek z wyniku:

Jest to tzw. wzór Herona. Uczony nie kończy jednak na zapisaniu pierwiastka – geodeta potrzebuje jakiegoś przybliżenia. Uczony podaje w tym celu pewien algorytm. Najbliższym pełnym kwadratem większym niż 720 jest liczba . Weźmy jako pierwsze przybliżenie naszego pierwiastka. Wiemy, że to za dużo. Możemy podzielić przez – gdyby to była prawidłowa wartość pierwiastka, to otrzymalibyśmy tę samą liczbę. Nasze przybliżenie jest z nadmiarem, po podzieleniu dostaniemy wynik z niedomiarem: . Bierzemy teraz średnią arytmetyczną obu przybliżeń i to będzie nasz wynik:

Heron kończy w tym miejscu, obliczając, że kwadrat ostatniej liczby jest trochę za duży. W postaci algebraicznej można by ten algorytm znajdowania zapisać następująco:

Jest on bardzo szybko zbieżny kolejne wartości to: – w trzecim przybliżeniu wszystkie cyfry są dokładne!

Heron nie tylko podał przepis na obliczanie pola trójkąta, ale także zamieścił jego dowód. Jak się zdaje, wyrażenie to znał już Archimedes, Heron nie przypisuje sobie zresztą pierwszeństwa. Ponieważ to jego praca się zachowała, mówimy o wzorze Herona. W dziejach nauki jest mnóstwo takich mylnie przypisywanych określeń. Tak wiele, że Michael Berry, znakomity fizyk matematyczny, sformułował kiedyś dwie następujące żartobliwe zasady:

Zasada Arnolda. Jeśli jakieś pojęcie nazwano czyimś imieniem, to nie jest to imię odkrywcy.

Zasada Berry’ego. Zasada Arnolda stosuje się do samej siebie.

(Chodzi o Vladimira Arnolda, też znakomitego matematyka.)

Podamy trzy dowody. Pierwszy, algebraiczny, znaleziony został przez uczonych arabskich i podawany był także przez Leonarda Pisano, zwanego Fibonacci (od filius Bonacci – syn Bonacciego) w XIII w. oraz Niccolò Fontanę, zwanego Tartaglia (Jąkała) w XVI w. Drugi będzie współczesny trygonometryczny. Trzeci, geometryczny, podany przez Herona, jest najmniej przejrzysty dla dzisiejszego czytelnika.

• Jest to właściwie dowód „siłowy”, wywodzący się z przekształceń formalnych.

Obliczamy brakującą wysokość trójkąta, wyrażając ją przez i korzystając z twierdzenia cosinusów. Można tu nie wprowadzać funkcji cosinus i korzystać wyłącznie z twierdzeń zawartych w Elementach Euklidesa.

Z tw. cosinusów mamy

Podstawiając to do wyrażenia wyżej i korzystając ze wzorów skróconego mnożenia, otrzymujemy wynik w postaci

• Punktem wyjścia dwóch pozostałych dowodów jest następująca obserwacja. Środek okręgu wpisanego w trójkąt leży na przecięciu dwusiecznych kątów trójkąta. Ponieważ dwie styczne poprowadzone z pewnego punktu na zewnątrz okręgu są tej samej długości, możemy łatwo wyrazić pole trójkąta jako sumę trzech prostokątów.

Wynika stąd, że pole trójkąta równe jest

Należy więc wyrazić przez długości boków.

Podejście trygonometryczne. Korzystamy z następującej tożsamości słusznej, gdy trzy kąty dają w sumie kąt prosty:

Do wykazania tego faktu wystarczy poniższy rysunek.

Zaczynamy od lewego niebieskiego trójkąta, potem dorysowujemy ten sam trójkąt, lecz przeskalowany (wszystkie boki razy ). Uzupełniamy rysunek do prostokąta. Trójkąt wewnątrz musi mieć kąt , a stąd wynika, że trzeci zaznaczony kąt równy jest . Możemy więc długości boków zapisać jak w wyrażeniach z prawej strony prostokąta. Równość obu boków prostokąta daje nam szukaną tożsamość (*).

Wracając do rysunku trójkąta z okręgiem wpisanym, łatwo zauważyć, że tangensy połowy kątów trójkąta znaleźć możemy z odpowiednich trójkątów prostokątnych, np. w niebieskim trójkącie, mamy

Wstawiając te wyrażenia do powyższej tożsamości, otrzymuje się wyrażenie na promień okręgu wpisanego, a stąd pole trójkąta.

• Na koniec przedstawimy oryginalny dowód Herona. Wiadomo, że nie jest to dowód samego Archimedesa, ponieważ uczony z Syrakuz nie używał pewnych środków technicznych tu użytych. Oto rysunek z pracy Herona w wydaniu filologicznym oraz jego przejrzystsza wersja z książki Geometry by Its History, A. Ostermanna i G. Wannera.

Mamy trójkąt z dwusiecznymi . Rysujemy dwie prostopadłe: do w wierzchołku oraz do w punkcie . jest w ten sposób przeciwprostokątną dwóch trójkątów prostokątnych oraz. Możemy więc na obu opisać wspólny łuk okręgu zaznaczony linią przerywaną. Rozważamy teraz kąty o wierzchołku w punkcie . Dwa z nich to i , co wynika z twierdzenia o kacie środkowym i kacie wpisanym opartym na tym samym łuku. Zatem kąt musi być równy , bo suma trzech kątów trójkąta równa się kątowi półpełnemu. Wobec tego kąt jest równy  . Mamy więc dwa podobne trójkąty prostokątne: oraz . Mamy stąd równość

Także trójkąty oraz są podobne (kąty wierzchołkowe w K). A więc

Porównując oba równania, wyznaczamy :

Promień jest wysokością trójkąta prostokątnego opuszczoną na przeciwprostokątną, mamy zatem

co pozwala natychmiast znaleźć pole trójkąta.

(*) Tożsamość, z której tu korzystamy, można także wyprowadzić w sposób czysto formalny bez żadnych rysunków. Mamy bowiem

korzystając najpierw ze wzoru na cosinus sumy, a następnie ze wzorów na cosinus oraz sinus sumy, dostaniemy:

Wystarczy teraz obie strony podzielić przez , aby uzyskać wynik.

Arystarch z Samos (przed 230 r. p.n.e.)

Archimedes wspomina o jego osobliwym poglądzie na wszechświat:

Wedle jego hipotez gwiazdy stałe oraz Słońce są nieruchome, Ziemia unoszona jest po kole wokół centralnie położonego Słońca, a sfera gwiazd stałych (mająca ten sam środek co Słońce) jest tak ogromna, iż koło, po którym według niego unoszona jest Ziemia, ma się do odległości gwiazd stałych jak środek sfery do jej powierzchni.

Następnie Archimedes udaje, że nie rozumie, o co chodzi: środek sfery to punkt, a więc nie jest w żadnej proporcji do promienia sfery. Arystarch najwyraźniej miał na myśli tylko tyle, że sfera gwiazd stałych musi być ogromna w porównaniu do orbity Ziemi, inaczej dostrzeglibyśmy, że gwiazdy przesuwają się w cyklu rocznym. Wymaganie takie było konieczne w każdej teorii heliocentrycznej, paralaksę roczną odkryto bowiem dopiero w 1838 roku, wcześniej było to technicznie niemożliwe. Pogląd Arystarcha nie przyjął się wśród greckich astronomów, można tylko spekulować, dlaczego tak się stało. Ścisła astronomia matematyczna Greków miała dopiero powstać. Najprawdopodobniej system geocentryczny pozwalał zdać sprawę z obserwowanych zjawisk, nie prowadząc do żadnych paradoksów i nie zmuszając naszej wyobraźni do gwałtownego przeskoku. Toteż poczekaliśmy na ów przeskok jeszcze trochę, bo aż do Kopernika, a właściwie Keplera i Galileusza.

Arystarch pochodził z Samos, tak jak Pitagoras, Azja Mniejsza i pobliskie wyspy (obecnie wybrzeże Turcji i wyspy greckie – okolice pojawiające się w newsach z powodu imigrantów) to kolebka naszej cywilizacji naukowej. W czasach Arystarcha, w pierwszej połowie III w.p.n.e., upłynęły już trzy wieki od Talesa z Miletu, nauka przeniosła się do Aleksandrii. Dwa pokolenia przed Arystarchem Euklides zebrał większość znanej wiedzy geometrycznej w Elementy, jedną z najważniejszych książek w dziejach ludzkości. Arystarch także przebywał w Aleksandrii, ale nie znamy szczegółów. To, co wiemy o tych greckich uczonych: ich najważniejsze dzieła, nie zawsze w całości, i prawie żadnych szczegółów biograficznych, bliskie jest ideałowi Alberta Einsteina. Sądził on, że liczą się tylko osiągnięcia, a błędy i biografia to rzeczy nieistotne.

Znany był jako Arystarch Matematyk, zapewne dla odróżnienia od imienników o odmiennych zainteresowaniach. Zachowała się jedna tylko jego praca: O rozmiarach i odległościach Słońca i Księżyca. Jak na matematyka przystało, szacuje on owe odległości z góry i z dołu. Największe znaczenie miało jego oszacowanie odległości Ziemia-Słońce w porównaniu do odległości Ziemia-Księżyc. Wyszło mu, że Słońce jest od nas 18 do 20 razy dalej niż Księżyc, a tym samym, że musi ono być mniej więcej tyle samo razy większe od naszego satelity, gdyż średnice kątowe obu ciał są jednakowe – wiemy to z przebiegu zaćmień Słońca. Liczby podane przez Arystarcha są mniej więcej 20 razy zaniżone, ale wynik ten przyjmowali wszyscy astronomowie aż do Kopernika. Kepler nieco je poprawił, ale też właściwie nic pewnego nie wiedział. Odległość Ziemia-Słońce wyznaczono poprawnie dopiero w drugiej połowie XVII wieku.

Istotę rozumowania Arystarcha przedstawia rysunek. Przyjął on założenie, że kiedy widzimy dokładnie połowę Księżyca, kąt między nim a Słońcem równy jest 87º. Dokładnie biorąc, nie używano wtedy stopni, Arystarch mówi, że kąt jest mniejszy od kąta prostego o 1/30 kąta prostego. Według naszej wiedzy trygonometrycznej, stosunek obu odległości równy jest

Co trzeba zrobić? Wystarczy wpisać w Google’a: sin(3 deg), a otrzymamy wynik: 0.0523359562. Wartość 1/sin(3 deg) jest równa mniej więcej 19. Oczywiście, w czasach Arystarcha nie było Google’a, nie było też pojęcia funkcji sinus, które z Indii przeszło do Arabów i następnie do Europy, ale dużo później. Używali go dopiero Regiomontanus i Kopernik, który pierwszy ogłosił tablice sinusów. Grecka trygonometria powstała dużo później niż działał Arystarch. A więc jak oszacować wielkość sinusa (my dla wygody będziemy używać funkcji trygonometrycznych i kątów wyrażonych w stopniach), kiedy nie mamy nic? Arystarch wiedział, jak szybko rosną sinusy i tangensy wraz z kątem. Można to przedstawić rysunkiem.

Widzimy z niego, że dodając takie same kąty, dodajemy coraz mniejsze wartości do sinusa (z lewej strony) i coraz większe odcinki do tangensa (z prawej strony). Nie wiemy, czy umiał tego dowieść, zachowane dowody tych faktów są dużo późniejsze. Intuicyjnie rzecz jest jednak jasna. Mamy nierówności:

 

Jedno oszacowanie jest proste:

Skorzystaliśmy z wartości sinusa 30º – a tę ostatnią można znaleźć, przepoławiając trójkąt równoboczny.

Do drugiego oszacowania można użyć funkcji tangens (oczywiście Arystarch mówił o pewnych proporcjach). Np.

Arystarch nie poszedł jednak na łatwiznę i znalazł oszacowanie dla , co pozwala ulepszyć wynik. Oto, jak rozumował, szukając tej wartości.

Mamy tu łuk okręgu o promieniu równym 1. Rysujemy dwusieczną kąta prostego, a potem jeszcze raz dwusieczną (linia kropkowana), szukaną wartość możemy odnaleźć w trójkącie prostokątnym ABC, który jest także równoramienny. Stosując twierdzenie Pitagorasa (rodaka z Samos), otrzymamy równanie kwadratowe, które pozwala wyrazić przez . Arystarch szukał czegoś prostszego, napisał więc następujące szacowanie:

opuszczając kwadraty po obu stronach i wyznaczając , dostajemy

Mamy więc wynik Arystarcha. Znaczył on, że Słońce jest wielkie w porównaniu z Księżycem, a także z Ziemią (oszacował on też odległość Księżyca od Ziemi). Być może z powodu wielkości Słońca, Arystarch zaczął rozważać hipotezę heliocentryczną: naturalniej wygląda, gdy mniejsze ciało krąży wokół większego niż odwrotnie. Wartość kąta 87º przyjęta była najprawdopodobniej tylko po to, żeby pokazać, że nawet jak się weźmie jakiś mały kąt, to można oszacować stosunki boków w trójkącie. Jak na matematyka przystało, nie przejmował się bardzo rzeczywistymi wartościami liczbowymi, jeśli nie są całkowite albo nie mają jakichś szczególnych własności. Ironią historii niedbałe szacowanie Arystarcha przetrwało aż po XVII wiek. Już po Arystarchu wyznaczono odległość Księżyca od Ziemi na 60 promieni ziemskich. Słońce byłoby więc w odległości 1200 promieni ziemskich. Przyjmując jeszcze, ze sfery planet powinny do siebie przylegać, wyznaczano wielkość wszystkich sfer aż do gwiazd stałych. Oczywiście, nic to nie miało wspólnego z rzeczywistością.

Nawiasem mówiąc wartość daje się wyrazić przez ułamki i pierwiastki z liczb całkowitych, co oznacza, że można ją uzyskać za pomocą jakiejś konstrukcji geometrycznej. Dokładne wyrażenie wygląda następująco:

ˆ