Adolphe Quetelet, krzywa dzwonowa i statystyczny człowiek (1835)

Był z wykształcenia matematykiem, z temperamentu organizatorem, lecz do historii przeszedł głównie dzięki swej niepohamowanej namiętności do stosowania metod statystycznych. Pragnął stworzyć statystyczną naukę o człowieku, opartą na rozmaitych szczegółowych spisach dotyczących narodzin, rozwoju, zdolności, karalności, chorób i zgonów ludnosci różnych obszarów czy grup. Jego dwutomowe dzieło z roku 1835 zatytułowane Sur l’homme et le développement de ses facultés, ou Essai de physique sociale („O człowieku i rozwoju jego zdolności, czyli zarys fizyki społecznej”) stało się szybko klasyczne. Quetelet wprowadził pojęcie statystycznego czy też przeciętnego człowieka (l’homme moyen), wyobrażając sobie, iż istnieje pewien idealny wzór, od którego poszczególni ludzie odchylają się za sprawą wielu różnych przyczyn. Pojęcie rozkładu statystycznego, który mieści całe spektrum badanej cechy, dopiero się kształtowało. Wcześniej  uczeni stosowali rozkłady statystyczne takie, jak rozkład Gaussa, do analizy błędów pomiarowych, gdy wiadomo, że mierzona wielkość przyjmuje pewną określoną wartość, a problemem jest jej ustalenie na podstawie obarczonych błędami pomiarów. Równolegle przebiegał społeczny proces uznania różnic między ludźmi za coś naturalnego, a nawet potrzebnego, nie za błąd w rozwoju czy niedostatek.

Jak to zwykle bywa w przypadku badań pionierskich, wiele wyników zostało potem zrewidowanych, niektóre stwierdzenia rażą dziś naiwnością. W swojej epoce był jednak Quetelet powszechnie uznawany za postać ważną, jego prace czytali uczeni tak różni, jak James Clerk Maxwell (który idee statystyczne zastosował do gazów) i Charles Darwin. Kontynuatorem prac Queteleta stał się kuzyn Darwina Francis Galton (to on ochrzcił rozkład Gaussa mianem rozkładu normalnego).

Znany powszechnie indeks masy ciała BMI (iloraz masy i kwadratu wzrostu) jest wynikiem obserwacji Queteleta, iż objętość ciała człowieka dorosłego nie jest proporcjonalna do sześcianu, lecz raczej do kwadratu wzrostu:

Gdyby człowiek rósł jednakowo we wszystkich wymiarach, ciężar w różnym wieku byłby proporcjonalny do sześcianu wzrostu. Obserwuje się jednak co innego. Wzrost masy jest mniej gwałtowny, z wyjątkiem pierwszego roku po urodzeniu, kiedy rzeczywiście na ogół obserwuje się powyższą proporcję. Potem jednak aż do okresu pokwitania ciężar ciała rośnie mniej więcej jak kwadrat wzrostu. (Sur l’homme, t. 2, s. 52)

Quetelet nie interesował się wszakże różnicami między ludźmi, starał się raczej odnaleźć typ idealny. Wskaźnik BMI zaczął być stosowany dopiero w drugiej połowie wieku XX, gdy problemem medycznym i ubezpieczeniowym w społeczeństwach zachodnich stały się nadwaga i otyłość.

W swym traktacie podał też Quetelet zaskakujący wzór na skłonność do przestępstwa (mierzoną statystycznie) jako funcję wieku w latach :

gdzie argument funkcji sinus podany jest w gradach: 100 gradów odpowiada kątowi prostemu. Wykres obserwowanej skłonności do przestępstwa wygląda u Qeteleta następująco:

źródło ilustracji: gallica.bnf.fr

Drugi wykres z płaskim obszarem szczytowym między trzydziestym a czterdziestym piątym rokiem życia dotyczy zdolności literackich. Wróćmy jeszcze do owej skłonności do przestępstwa.

Zależność Queteleta jest iloczynem dwóch funkcji: malejącej funkcji w pierwszej ćwiartce (czyli czegoś zbliżonego do paraboli) oraz funkcji logistycznej, która opisuje szybki wzrost w okolicy . Nb. krzywa logistyczna zastosowana została kilka lat później przez Pierre’a François Verhulsta, ucznia Quteleta, do modelowania ograniczonego wzrostu populacji, który zaczyna się wykładniczo (nieograniczone rozmnażanie), lecz osiąga naturalną barierę (np. brak pożywienia). Tutaj, w pracy Queteleta, krzywa logistyczna zdaje sprawę z osiągania dojrzałości przez człowieka, na dobre i złe. Oczywiście, nie powinniśmy zbyt serio traktować tego wzoru. Sam Quetelet w późniejszych latach ograniczał się do opisu danych statystycznych, nie upierając się przy żadnym wyrażeniu.

Wykres skłonności do przestępstw wg płci. Widzimy, że kobiety wkraczają później na ścieżkę kryminalną, lecz dłużej są aktywne.

Trwałym dorobkiem Queteleta okazało się stosowanie krzwej dzwonowej do opisu rozkładu statystycznego. Sam po raz pierwszy zastosował ją do statystyki obwodu w piersiach szkockich rekrutów. Jego dane wyglądały następująco:

Obwód w klatce piersiowej wyrażony jest w calach. Quetelet starał się dopasować do tych danych krzywą Gaussa, lecz w praktyce użył rozkładu dwumianowego z prawdopodobieństwami sukcesu/porażki oraz liczbą prób równą 999 (tak, żeby mieć 1000 różnych wyników). Inaczej mówiąc, są to prawdopodobieństwa uzyskania orłów w 999 rzutach monetą.

Jako uczeń Fouriera i Laplace’a wiedział dobrze, że rozkład dwumianowy dąży przy dużych wartościach liczby prób do rozkładu Gaussa. W ten sposób zaczęła się oszałamiająca kariera krzywej Gaussa w zastosowaniach statystycznych. W latach późniejszych przesadne stosowanie rozkładu Gaussa do wszelkich możliwych danych zaczęto nawet nazywać „quetelizmem” – bo, oczywiście, istnieją też inne rozkłady, choć w wielu sytuacjach właśnie rozkład Gaussa prawidłowo opisuje stan faktyczny.

Newton, Leibniz i liczba pi z szeregu Fouriera

Pisałem niedawno o szeregach odkrytych przez Leibniza i Newtona, a związanych z liczbą . Oba te szeregi można łatwo powiązać ze sobą za pomocą rozwinięcia Fouriera. Kiedyś już pisałem o Josephie Fourierze i jego nieśmiertelnym wynalazku. Tutaj pokażemy tylko, jak to się wiąże z szeregami Leibniza:

i Newtona:

Rozwinięcie w szereg Fouriera stosuje się do funkcji okresowych. Weźmy np. funkcję w przedziale .

Możemy zrobić z niej funkcję okresową powtarzając jedynie zęby piły na kolejnych przedziałach. Funkcja ta jest nieciągła na końcach przedziałów, ale to nie szkodzi. Idea Fouriera polega na przybliżeniu dowolnej funkcji nieskończoną sumą sinusów i cosinusów o coraz mniejszych okresach. W naszym przypadku okresem jest , a funkcja jest nieparzysta, jak sinus. Szukamy więc rozwinięcia następującej postaci:

Żeby znaleźć wartości współczynników rozwinięcia, mnożymy obie strony przez . Ponieważ całka po okresie z iloczynu dwóch sinusów znika, więc z prawej strony przeżywa tylko wyraz (*):

Ostatnia równość po prawej stronie wynika stąd, że kwadrat sinusa scałkowany po wielokrotności okresów daje razy długość przedziału całkowania.
W naszym przypadku

gdzie cały czas ograniczamy się do przedziału . Proszę zobaczyć, co otrzymamy, biorąc coraz większe liczby składników sumy.

Widać gołym okiem, że szereg jest zbieżny oprócz może końców przedziału, gdzie nasza funkcja ma skok.
Teraz wystarczy wziąć dwie wartości argumentu. Dla otrzymamy szereg Leibniza, dla – szereg Newtona. Warto zauważyć, że jesteśmy daleko od końców przedziału, gdzie mogą być kłopoty ze zbieżnością. Oczywiście Joseph Fourier to już XIX wiek, czyli matematyka bogatsza o 150 lat rozwoju od czasów Leibniza i Newtona. Najprostszy znany mi wykład o szeregach Fouriera znaleźć można w rozdz. 50 t.1 Wykładów Feynmana.

(*) Wynika to z tożsamości:

Całka z cosinusa po okresie równa jest zero, więc tylko pierwszy wyraz po prawej stronie dla przeżywa całkowanie.

Wieczny powrót od Retyka i Kopernika do Poincarégo

Niebo Greków składało się z wirujących z różną prędkością sfer. Jak pisał Platon w Timajosie:

…aby dać jasną miarę relatywnej powolności i szybkości, z którymi gwiazdy wykonują swoich osiem ruchów, Bóg umieścił na drugiej po Ziemi orbicie światło, które nazywamy teraz Słońcem, aby całe niebo było oświetlone, a jestestwa żyjące, wszelkie, jakie natura zamierzyła, mogły uczestniczyć w Liczbie, ucząc się arytmetyki przez obroty Tego Samego i podobnego. (…)  A na obieg innych gwiazd ludzie, z bardzo małymi wyjątkami, nie zwracają uwagi, nie nadają im nazw, nie porównują ich obiegów ilościowo, tak, że powiedzieć można, nie wiedzą, że czas to błędne wędrówki tych gwiazd nieprzeliczone i przedziwnie różnorodne. Mimo to można pojąć, że doskonała liczba czasu wypełnia rok doskonały wtedy, gdy wszystkie osiem obrotów, mających swoje względne stopnie szybkości, dokona się wspólnie i zakończy w tym samym czasie, mierzonym obrotem Tego Samego, które się porusza w sposób jednostajny. (39 c-39d)

Według Platona po 36 000 lat cykl kosmiczny się powtarza. W XVI w. Georg Joachim Retyk, jedyny uczeń Kopernika, powiązał epoki historyczne ze zmianami mimośrodu orbity Ziemi. Środek orbity Ziemi poruszał się bowiem u Kopernika po niewielkim kółku , a okres tego ruchu wynosił 3434 lat egipskich. Kiedy mimośród orbity Ziemi był największy Rzym stał się z republiki cesarstwem. Po ćwierci obiegu owego małego kółka powstał islam, a po następnej ćwierci ok. 1652 r. – upadnie, jak prorokował. Drugie przyjście Chrystusa miało nastąpić w roku 2510, gdy mimosród wróci po raz drugi do swej wartości w chwili stworzenia. W książce Kopernika nie znajdziemy rozważań tego typu. Nie ma jednak podstaw by sądzić, że ich nie aprobował. Astrologia była dziedziną respektowaną, głównym powodem badania położeń planet na niebie. Więc choć Kopernik nie był z pewnością entuzjastycznym astrologiem – nie zachowały się tworzone jego ręką horoskopy, to mógł wierzyć, że los Ziemi i jej mieszkańców jest powiązany ze zjawiskami niebieskimi. O obrotach było dziełem czysto astronomicznym i matematycznym, zatem umieszczanie w nim astrologicznych konkretów byłoby nie na miejscu.

Środek orbity Ziemi porusza się po małym kółku, rzeczywiste Słońce spoczywa sobie spokojnie obok, nie biorąc udziału w tych „rewolucjach”. Słowo użyte przez Kopernika w tytule De revolutionibus oznaczało obroty, a więc coś cyklicznego, z czasem zaczęło oznaczać wszelkie dramatyczne przemiany, na ogół już jednokierunkowe. Proporcje na rysunku są oczywiście przesadzone, inaczej niewiele byłoby widać.

Wraz z upadkiem idei sfer niebieskich znaczenie cyklów planetarnych zmalało, a czas zaczął wydawać się nieskończony niczym prosta euklidesowa: od minus do plus nieskończoności. Oczywiście, chrześcijanie obowiązani byli wierzyć w stworzenie świata i jego koniec, ale z braku dopływu nowych bodźców wiara ta wyraźnie słabła. Już w XVIII wieku niezbyt się buntowano, gdy Buffon obliczył wiek Ziemi na mniej więcej dziesięć razy dłuższy, niż wynikałby z Biblii. Potem Fourier, zajmując się stygnięciem Ziemi, jeszcze powiększył tę wartość. Mechanistyczny wszechświat najłatwiej było sobie wyobrażać jako trwający od zawsze i mający istnieć zawsze. Od połowy XIX w. do obrazu tego doszły dwie zasady termodynamiki. Według pierwszej – zasady zachowania energii – istnieje wielkość, która we wszystkich przemianach się nie zmienia, co przemawia za tym, że wszechświat nie ma końca. Według drugiej zasady energia rozkłada się z czasem coraz bardziej równomiernie, świat powinien stawać się jednolitym ośrodkiem o stałej gęstości i temperaturze. Tak więc choć istniałby zawsze, po pewnym czasie przechodziłby w postać mało interesującą i praktycznie martwą. Mówiło się o „śmierci cieplnej” wszechświata.

Pomysł wiecznego powrotu pojawił się w latach osiemdziesiątych XIX stulecia nie u uczonego, lecz u filozofa, Friedricha Nietzschego. Pisał on:

Jeśli wszechświat należy uważać za pewną ilość energii, za pewną liczbę ośrodków energii, a każda inna koncepcja pozostaje nieokreślona i przez to bezużyteczna, to wynika stąd, że wszechświat przejść musi przez obliczalną liczbę kombinacji w wielkiej grze losowej, którą jest jego istnienie. W nieskończoności, w takim albo innym momencie, zrealizowana musi zostać każda możliwa kombinacja; a nawet więcej: musi ona zostać zrealizowana nieskończenie wiele razy. (…) wszechświat ukazuje się więc jako ruch kolisty, który zdążył się już powtórzyć nieskończenie wiele razy i który toczy swą grę przez całą wieczność.

Nietzsche, pogrążający się już w szaleństwie, przekonany był, że rozumowanie takie przeczy mechanistycznej nauce, którą traktował pogardliwie. Jednak w roku 1889 Henri Poincaré udowodnił, że w newtonowskiej mechanice także mamy do czynienia z wiecznym powrotem. Jego rozprawa zatytułowana O problemie trzech ciał i równaniach dynamiki zawierała nowatorskie podejście do klasycznego tematu za pomocą metod topologii, czyli rozważań operujących ogólnymi pojęciami takimi jak ciągłość, które okazały się bardzo owocne. Poincaré stał się prekursorem teorii chaosu. A metody topologiczne wykazywały jeszcze nieraz swą przydatność: np. w badaniu osobliwości w ogólnej teorii względności (czarne dziury, początek wszechświata) czy w badaniach osobliwych stanów materii (Nobel 2016).

Poincaré udowodnił następujące twierdzenie: Jeśli dopuszczalne stany układu mechanicznego zawarte są w pewnym ograniczonym obszarze D, to w dowolnym otoczeniu U każdego punktu obszaru D znajdzie się punkt s, który powraca do otoczenia U.

Można to narysować. Przestrzeń stanów to zbiór punktów, których współrzędnymi są położenia i pędy (same położenia nie wystarczą, bo nie precyzują, jak zachodzi ruch; jest to tzw. przestrzeń fazowa układu). Naszym obszarem jest niebieska elipsa (obszar ograniczony odpowiada temu, że np. energia układu jest stała). Rozpatrujemy dowolnie mały obszar 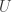(u nas ma postać czerwonego kółka). Stany z obszaru 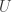po jakimś kroku czasowym przechodzą w stany , niemające wspólnego punktu z 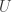(gdyby tak nie było, to już mamy tezę twierdzenia). Po kolejnych krokach czasowych otrzymujemy . Wiadomo z mechaniki, że objętości tych wszystkich obszarów są jednakowe (twierdzenie Liouville’a). Skoro tak, to któryś z obszarów ciągu 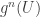musi przeciąć się z 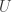, a tym samym istnieć będzie punkt należący zarówno do U, jak i (*)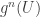

Oznacza to, że wybierając dowolny stan początkowy i czekając dostatecznie długo, doczekamy się powrotu naszego układu jeśli nie do punktu początkowego to dowolnie blisko tego punktu. Wynik jest zupełnie ogólny, nie musimy nic wiedzieć na temat działających sił, a nasz układ może być dowolnie duży. Twierdzenie Poincarégo pokazuje więc, że na gruncie mechaniki mamy do czynienia z wiecznym powrotem. Można pokazać, że powroty takie będą się powtarzać nieskończenie wiele razy. Idea powrotu nie przeczy więc mechanicznemu światu, choć niezgodna jest ze śmiercią cieplną wszechświata. Poincaré zauważył filozoficzne konsekwencje swego twierdzenia. Zauważył je także młody matematyk Ernst Zermelo, asystent Plancka, który wystąpił z polemiką przeciwko koncepcji entropii Boltzmanna. Zermelo dał się potem poznać jako wybitny specjalista od podstaw matematyki, jego aksjomaty teorii mnogości stosowane są dziś powszechnie.

(*) Idea dowodu twierdzenia Poincarégo opiera się na zachowaniu objętości w przestrzeni fazowej. Kolejne zbiory 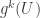mają takie same objętości, nie mogą więc być parami rozłączne, gdyż wtedy suma ich objętości przekroczyłaby każdą zadaną liczbę, a wszystko musi się zmieścić w większym obszarze . Jeśli zaś jakaś para tych obszarów nie jest rozłączna, np. przy pewnych , to 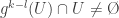, co oznacza, że dla jakiegoś punktu mamy , gdzie .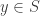

Zachowanie objętości kolejnych obszarów wynika stąd, że gdybyśmy wyobrazili sobie punkty przestrzeni fazowej jako punkty w poruszającej się cieczy, to dywergencja pola prędkości owej cieczy równa się zeru, a to jest warunek dla cieczy nieściśliwej, czyli zachowującej objętość. Oznaczając wektor prędkości 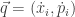dla 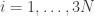(gdzie 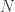jest liczbą cząstek składających się na układ), mamy

gdzie jest hamiltonianem układu, po wskaźniku 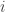sumujemy.

Dodatek matematyczny, twierdzenie Poincarégo w nowoczesnym sformułowaniu. Ujęcie to zawdzięczamy Constantinowi Carathéodory’emu, matematykowi z Getyngi, był już rok 1919. Pojawiło się pojęcie miary, będące uogólnieniem zwykłej objętości. Twierdzenie Poincarégo można uściślić w ten sposób, że zbiór punktów przestrzeni fazowej, które nigdy nie powracają do wybranego otoczenia jest miary zero. Zbiory miary zero, czyli zerowej objętości, mogą mieć skomplikowaną strukturę, ale są rzadkie w tym sensie, że nie można im przypisać żadnej dodatniej objętości. Nowoczesne pojęcie miary zbioru rozszerza dodawanie miar na zbiory przeliczalne (dające się ponumerować liczbami naturalnymi, ciągi zbiorów). Miara spełnia więc warunek:

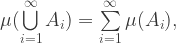
gdy zbiory są parami rozłączne: , dla różnych wskaźników 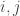. Pokażemy, że jeśli odwzorowanie g zachowuje miarę, a miara obszaru D jest skończona, to miara zbioru tych punktów D, które nie mają własności powracania, jest równa zeru. W tym sensie prawie każdy stan ma własność powracania.

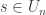Dla dowodu pokrywamy obszar D przeliczalną liczbą kul . Dla każdej kuli definiujemy jej podzbiór jako zbiór tych , dla których 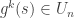tylko dla skończenie wielu wartości wskaźnika 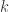. Zbiór jest zbiorem punktów niepowracających. Ponieważ 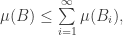wystarczy udowodnić, że każdy ze zbiorów jest miary zero.

W tym celu wybierzmy dowolny wskaźnik 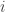. Będziemy teraz pisać oznaczenia 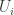bez indeksu dla  uproszczenia zapisu.

Rozpatrzmy zbiór . Punkt 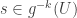wtedy i tylko wtedy, gdy oraz przy 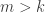. Zbiory są parami rozłączne, gdy wskaźniki 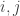są różne, przy czym dopuszczamy, aby któryś z nich równał się zeru (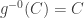). Zbiór 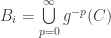. Zatem mamy

Miary wszystkich zbiorów po prawej stronie są takie same, bo nasze odwzorowanie zachowuje miarę. Gdyby miary te były dodatnie, suma byłaby nieskończona, co jest niemożliwe, gdyż , więc jego miara musi być skończona. Zatem wszystkie miary po prawej stronie są zerowe i 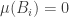. Zbiór 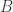jest przeliczalną sumą , zatem i on musi być miary zero. Dowód ten pochodzi z artykułu R. Daniela Mouldina, Probability and Nonlinear Systems, „Los Alamos Science” nr poświęcony Stanisławowi Ulamowi.

Twierdzenie Poincarégo o powracaniu ilustruje tzw. kot Arnolda (chodzi o Vladimira Arnolda, wybitnego matematyka rosyjskiego). Mamy tu ograniczoną przestrzeń stanów i pewną grupę stanów początkowych, które ułożone są w kształt kociego pyszczka. Gdy puścimy w ruch tę animację, zobaczymy, że w pewnych chwilach kot powraca.

 

Nieśmiertelny wynalazek Josepha Fouriera (1804-1822)

Fourier, syn krawca, którego wcześnie odumarli rodzice, wszystko zawdzięczał swemu talentowi, a także umiejętności niezrażania sobie ludzi. Jego kariera wiele mówi o Francji tamtych czasów. Urodził się i wychowywał za panowania Ludwika XVI. Ktoś zwrócił uwagę na zdolnego chłopca i polecił go biskupowi Auxerre. Dzięki protekcji duchownego Fourier został przyjęty do szkoły artyleryjskiej kierowanej przez maurystów (benedyktyńska kongregacja św. Maura). Wcześnie ujawnił talent matematyczny. Zabiegał o przyjęcie na służbę do artylerii, lecz mimo poparcia słynnego matematyka Adrien Marie Legendre’a, minister odmówił. „Fourier, nie pochodząc ze szlachty, nie ma wstępu do artylerii, choćby nawet był drugim Newtonem” – oświadczył minister. Młody człowiek wstąpił więc do nowicjatu u maurystów, ale wybuchła Rewolucja Francuska i Fourier zmienił zdanie. Ojcowie zatrudnili go mimo to w swej szkole artyleryjskiej, gdzie uczył matematyki, a jak było trzeba, to także retoryki, filozofii i historii. Należał do słuchaczy École normale roku III: był to swoisty eksperyment szkolny, mający dostarczyć Rewolucji nowy zastęp nauczycieli. Tysiąc pięciuset uczniów słuchało wykładów największych uczonych Francji: Lagrange’a, Laplace’a, Monge’a, Bertholleta. Prawdziwą karierę zrobił Fourier dopiero za czasów Napoleona: był wśród uczonych towarzyszących Pierwszemu Konsulowi w wyprawie egipskiej („Osły i uczeni do środka” – wołali oficerowie, kiedy konwój Francuzów został zaatakowany na pustyni). Fourier został sekretarzem Instytutu Egipskiego powołanego przez Napoleona, wniósł swój wkład do jego publikacji. Po kapitulacji armii i powrocie do Francji, został prefektem departamentu Izery, gdzie budował drogi i osuszył bagna Bourgoin. W tym czasie dobiegający czterdziestki uczony zajął się poważniej fizyką matematyczną: zagadnieniem rozchodzenia się ciepła. W roku 1807 wygrał konkurs Akademii Nauk poświęcony temu zagadnieniu. W roku 1822 opublikował swą słynną monografię Théorie analytique de la chaleur – „Analityczną teorię ciepła”.

Wiedza o cieple nie była zbyt wielka: znano pojęcie temperatury i ciepła właściwego. Nie wiedziano, czym jest ciepło, wyobrażano sobie, że jest rodzajem nieważkiej cieczy, która przepływa z jednego ciała do drugiego, nie ginąc ani nie powstając (zasady termodynamiki sformułowano trzydzieści lat później). Fourier przyjął, że strumień ciepła na jednostkę powierzchni i czasu zależy od tego, jak szybko zmienia się temperatura z odległością.

Szybkość zmiany temperatury to gradient. Strumień ciepła jest więc proporcjonalny do gradientu temperatury: jeśli ten sam spadek temperatury przypada na dwa razy krótszy odcinek, to strumień będzie dwa razy większy. Znak minus informuje, że ciepło płynie od temperatury wyższej do niższej, a nie odwrotnie. Stała charakteryzuje materiał.
Będziemy szukali przepływów stacjonarnych, tj. takich, które nie zależą od czasu. Jeśli przepływ ciepła jest jednowymiarowy, tzn. strumień jest wyłącznie w kierunku osi x, to łatwo stwierdzić, że stacjonarność oznacza wówczas stałość . Powierzchnie izoterm to płaszczyzny prostopadłe do osi , a gradient temperatury jest stały.
Znacznie ciekawsza jest sytuacja w przypadku 2D. Wyobraźmy sobie prostokąt o bokach . W naszym przypadku stacjonarnym całkowita ilość ciepła wypływająca w jednostce czasu z prostokąta musi być równa zeru: inaczej prostokąt ogrzewałby się albo oziębiał z czasem.

Warunek ten zapisany matematycznie oznacza, że

W pierwszym wierszu mnożymy strumienie przez długości odpowiedniego boku prostokąta, aby otrzymać ilość ciepła przechodzącą przez daną krawędź. Korzystając z tego, że strumień związany jest z gradientem, otrzymujemy następujący warunek stacjonarnego przepływu:

Jest to równanie Laplace’a, występujące też w elektromagnetyzmie i teorii grawitacji. Aby zrozumieć jego sens, można wyobrazić sobie punkt płaszczyzny otoczony przez cztery inne punkty oddalone o niewielką odległość .

Równanie Laplace’a mówi, że średnia arytmetyczna temperatur w punktach czerwonych równa się temperaturze w środkowym punkcie niebieskim. Nie powinno to dziwić: chodziło przecież o to, aby ciepło nie gromadziło się w żadnym obszarze ani z niego nie uciekało (**). Biorąc odpowiednio małe , można w ten sposób rozwiązać równanie Laplace’a numerycznie. Można pokazać ogólnie, że gdy funkcja spełnia równanie Laplace’a, to jej średnia wartość po małej sferze (u nas okręgu) o promieniu równa jest wartości w środku sfery.

Wśród zagadnień rozważanych przez Fouriera znalazło się i takie: mamy nieskończony dwuwymiarowy pasek, którego jeden bok utrzymywany jest w temperaturze 1, a dwa boczne w temperaturze 0 (odpowiadały one w naszej skali oraz ). Zakładamy też, że w nieskończoności temperatura spada do zera. Szukamy rozwiązania stacjonarnego.

Łatwo można znaleźć rozwiązania, w których temperatura na obu bokach równa jest zeru oraz stopniowo spada:

gdzie parametr jest całkowity. Dla wygląda to tak:

Dla mamy jednak funkcję zdecydowanie różną od stałej. Łatwo sobie wyobrazić, że tak będzie i dla innych wartości . Idea Fouriera polegała na tym, aby temperaturę wzdłuż osi przedstawić jako sumę nieskończenie wielu sinusów:

Tak wygląda suma pierwszych trzech wyrazów:

A tak ośmiu:

Naprawdę nasza suma sinusów jest nieparzysta i wygląda następująco (osiem składników):

Jest to funkcja o okresie . Podejście Fouriera spotkało się z niedowierzaniem i krytyką. Wprowadzał on do rozważań „dziwne” funkcje, które nie są określone jednym wzorem i nie są ciągłe, przybliżając je wszystkie czymś tak banalnie prostym jak sinusoidy. Wiele prac z dziedziny fizyki i matematyki wyrosło z podejścia Fouriera. Matematycy zastanawiali się nad zbieżnością i pojęciem funkcji, fizycy i inżynierowie stosowali w praktyce. Dziś traktujemy szereg Fouriera jak przedstawienie wektora za pomocą pewnych wektorów bazowych. Np. każdy wektor na płaszczyźnie możemy przedstawić jako kombinację dwóch jednostkowych wektorów o kierunkach osi x i y. Funkcje okresowe o okresie wyrażają się przez funkcje i , które pełnią rolę wektorów bazowych. Przestrzeń tak zdefiniowana jest nieskończenie wymiarowa i nazywa się przestrzenią Hilberta. Z punktu widzenia fizyka czy inżyniera analiza fourierowska pozwala rozłożyć każdy impuls okresowy na składowe, co pozwala wiele zrozumieć. Np. wysokość tonu wydawanego przez instrument muzyczny określona jest pierwszym sinusem, a następne przesądzają o barwie dźwięku: po tym odróżniamy a zagrane na fortepianie od a zagranego na skrzypcach.

Kiedy już mamy naszą dziwną funkcję rozwiniętą w szereg Fouriera, wystarczy zsumować nieskończenie wiele rozwiązań takich jak (*). Pierwsze trzy składniki dadzą rozwiązanie poniżej (możemy zawsze w razie potrzeby użyć większej liczby wyrazów).

(**) Związek średniej arytmetycznej z równaniem Laplace’a wynika z rozwinięcia w szereg Taylora z dokładnością do :

Biorąc średnią arytmetyczną z tych czterech wyrażeń i odejmując wartość , otrzymujemy