Henry Pemberton, lekarz i członek Royal Society, wspominany dziś bywa jedynie dlatego, że był redaktorem III wydania Newtonowskich Principiów, ostatniego za życia wielkiego człowieka. Biegły był nie tylko w medycynie, ale i matematyce oraz fizyce ówczesnej i przy okazji pewnej polemiki zwrócił na siebie uwagę sędziwego sir Isaaca. My przedstawimy tu krótko jego pracę z 1722 r., zawierającą wyjaśnienie nadliczbowych łuków tęczy pojawiających się czasem wewnątrz pierwszego łuku Kartezjańskiego. Isaac Newton wprowadził swego czasu hipotezę przystępów łatwego odbicia i załamania dla promieni światła. Wprowadzała ona do optyki geometrycznej element okresowości przestrzennej, ale bez wspominania o falach. Zjawiska falowe nie były w XVII w. zbyt dobrze rozumiane nawet tzw. falowa teoria Huygensa dotyczyła nieokresowych zaburzeń w eterze, czegoś w rodzaju fal uderzeniowych. Pomysł Newtona był taki, że po załamaniu w ośrodku promień nabierał własności okresowych i dlatego napotykając następną powierzchnię, mógł się odbić albo załamać – w zależności od tego, czy był właśnie w przystępie łatwego odbicia, czy załamania. Mogło to jego zdaniem wynikać z oddziaływania cząstek światła z falą wzbudzoną przez nie w ośrodku (niczym fale na wodzie, do której wpadł kamień), która to fala rozchodziła się szybciej od światła i niejako decydowała, czy zostanie ono przepuszczone, czy odbite. Owe mityczne przystępy bądź napady (fits) objaśniać miały bardzo konkretne wyniki doświadczeń z interferencją w cienkich warstwach. Idea była jednak na tyle karkołomna i spekulatywna, że pomimo bałwochwalczego stosunku rodaków do myśli dożywotniego przewodniczącego Royal Society nie bardzo się przyjęła. Pemberton, wczuwając się w świat Newtonowskich idei, wpadł na pomysł, że owe przystępy mogłyby wyjaśnić nadliczbowe łuki tęczy.

Niech BCD będzie drogą promienia ekstremalnego, wyznaczającego granicę tęczy (rysunek zaczyna się od punktu odbicia w kropli B). Można podejrzewać, że oprócz BC biegną z tego punktu także jakieś słabsze promienie BE, BG, BF i BH. Zauważmy, że łamią one prawo odbicia. Jeśli już się z tym pogodzimy, to można rozumować następująco: promień BCK (kartezjański) przechodzi granicę woda-powietrze, więc musi być w przystępie załamania. Pobliskie promienie BG i BE będą w takim razie w przystępie odbicia i odbiją się wewnątrz kropli, nie wychodząc z niej przynajmniej na razie. Możemy sobie jednak wyobrazić nieco dalszą parę promieni BF i BH, takich że akurat są w przystępie załamania i wyjdą z kropli równolegle do siebie. One właśnie utworzą pierwszy łuk nadliczbowy (bo oczywiście ich kąt odchylenia musi być mniejszy od ekstremalnej wartości 42°). W dodatku, ponieważ odległość owych przystępów zależy od barwy, więc i promień tego łuku będzie zależał od barwy. Tyle udało się Pembertonowi. Na osiemdziesiąt lat zapadła cisza, przerywana jedynie monotonią podręczników, które ubarwiały tęczę po swojemu. Tłumaczono np. łuki nadliczbowe obecnością cząstek siarki (w szerszym pojęciu niż dzisiaj: siarka nie była jeszcze pierwiastkiem chemicznym, lecz niemal uniwersalnym składnikiem materii). Itd. itp. Przypominał to nieco niektóre wyjaśnienia sprzed Descartes’a, gdy zamiast zrozumieć kąt 42°, podawano w wątpliwość obserwacje. Zresztą nawet Descartes w swej Meteorologii asekurancko dodawał, że kąt może się różnić od znalezionego przezeń z powodu odmiennych warunków pogodowych. Rzecz w tym, że nie może, temperatura słabo wpływa na współczynnik załamania wody, a nic innego tu nie wchodzi w grę.
W ten sposób dochodzimy do Thomasa Younga, także lekarza, ale i uniwersalnego uczonego. Postaci takich jak Young w Polsce nie miewaliśmy. Stąd może Royal Society od XVII w. z jednej strony, a cud w Parczewie w wieku XXI z drugiej. I nie chodzi tu bynajmniej o religijność. Young wywodził się z rodziny kwakierskiej, choć w wieku dorosłym był już standardowo , tzn. anglikańsko, religijny. Był człowiekiem obsesyjnie skupionym na faktach, nastawionym empirycznie, znającym także matematykę, a do tego cały zestaw języków nowożytnych i starożytnych. Rzeczowość, nawet pedanteria, brak błyskotliwości, niestrudzona pracowitość, rozległa, zaiste encyklopedyczna wiedza (zdawało się, że mógłby samodzielnie zostać kompetentnym autorem całej encyklopedii powszechnej, pisał zresztą artykuły do Encyclopedia Britannica na imponujący zestaw najprzeróżniejszych tematów). Z tego pracowitego żywota (zajmował się także praktyką lekarską, choć był finansowo niezależny) dziś pamiętamy głównie zasadę interferencji światła i resuscytację falowej teorii światła. Doświadczenie Younga zostało uznane za najpiękniejszy eksperyment w fizyce: światło z dwóch wąskich szczelin interferuje ze sobą, dając prążki na ekranie. Wykonywano takie doświadczenia nie tylko ze światłem, ale i z elektronami, a nawet fullerenami, ukazuje ono bowiem coś więcej niż falowość światła: falowość wszelkich cząstek mikroświata. Young nie wykonał takiego idealnego eksperymentu, był on dla niego bardziej ideą wywiedzioną z doświadczeń i pomiarów, niż sprawozdaniem laboraoryjnym. W tym, co obserwował, pomieszane były skutki interferencji z dwóch otworów z dyfrakcją na samych otworach. Najbliżej sytuacji idealnej był wówczas, gdy światło słoneczne z małego otworka skierował na ustawioną krawędzią kartę tekturową. Na ekranie pojawiły się prążki, które znikały, gdy zasłonić jedną ze stron wiązki.

Young wiedział już wówczas, że aby uzyskać maksimum natężenia, różnica dróg optycznych dwóch promieni światła musi być całkowitą wielokrotnością długości fali. Gdy różnica dróg jest połówkową wielokrotnością, otrzymujemy minimum. Wiedział też, że droga w ośrodku o współczynniku załamania n musi być liczona n-krotnie, co wynika stąd, że w takim ośrodku długość fali zmniejsza się się n razy.
Nie będziemy opisywać rozmaitych badań optycznych Younga, pokażemy tylko jedną z plansz do jego wykładów. Prowadził on przez kilka lat popularne wykłady w Royal Institution. Uczęszczali na nie po pracy londyńscy rzemieślnicy bądź urzędnicy, ale także i damy z wyższych sfer. Wykłady Younga dotyczyły całości filozofii naturalnej, a także elementów matematyki. Ukazują stan wiedzy dwa wieki temu.


Więcej plansz Younga można znaleźć tutaj.
Young objaśnił nadliczbowe łuki tęczy interferencją promieni takich, jak na rysunku. Dwa równoległe promienie załamują się w kropli, a następnie po odbiciu ją opuszczają także jako równoległe. Ponieważ są to promienie, które odchylają się mniej niż promień Descartes’a efekt ich interferencji widoczny będzie pod kątem mniejszym, niż słynne 42°.

Wyjaśnienie to przedstawił w roku 1803 podczas wykładu Bakera w Royal Society, jednakże bez rysunku i żadnych obliczeń. Więcej informacji znalazło się w jego artykule do Encyclopedia Britannica Supplement zatytułowanym Chromatics napisanym w 1817 r. Różnica dróg optycznych dla dwóch promieni na rysunku równa się

Przyjęliśmy promień kropli równy 1. Young przedstawił tabelkę różnic drogi optycznej dla współczynnika załamania  odpowiadającego skrajnej czerwieni.
odpowiadającego skrajnej czerwieni.

Tabelka ułożona jest wg odległości kątowych od krawędzi tęczy. A więc (przykład Younga), jeśli czerwień pierwszej dodatkowej tęczy pojawi się o 2° od czerwieni tęczy głównej, to oznacza to, że drogi obu promieni różnią się o długość światła czerwonego  (wartość zmierzona przez Younga). Znajdujemy w tabelce pozycję 2° i odczytujemy, że kąty załamania (i zarazem odbicia) dla obu promieni równają się wtedy 42°59′ i 36°23, a różnica dróg 0,004. Znaczy to, że promień kropel wynosi
(wartość zmierzona przez Younga). Znajdujemy w tabelce pozycję 2° i odczytujemy, że kąty załamania (i zarazem odbicia) dla obu promieni równają się wtedy 42°59′ i 36°23, a różnica dróg 0,004. Znaczy to, że promień kropel wynosi

Widzimy praktyczny cel owej tabelki: obserwator tęczy mógł sobie obliczyć, jakiej wielkości krople wywołały zjawisko. Uczony zadał sobie sporo pracy, szukając numerycznie kątów odpowiadających zadanym odległościom od krawędzi tęczy. Warunek Younga na maksima można zatem zapisać w postaci

Sam unikał matematyki tak długo, jak się dało, co było skutkiem pewnego przesądu. Otóż twierdził on, że wysoce zmatematyzowana fizyka w postaci algebraicznej, uprawiana zwłaszcza na kontynencie, jest czymś w rodzaju sztucznych ułatwień dla myśli, która zaczyna prześlizgiwać się po temacie zamiast go precyzyjnie ogarnąć. „Wydaje się wręcz, że matematyczna uczoność stanowi coś w rodzaju eutanazji talentu fizycznego”. Wygłosił on tę opinię w biogramie Josepha Lagrange’a, co chyba nie było ani trafne, ani dobrze usytuowane.
Oczywiście, prace uczonych takich jak Euler, Lagrange czy Laplace (z których Young także korzystał) mogły czasem sprawiać wrażenie przesadnego zmatematyzowania. Ale to samo było kiedyś z Isaakiem Newtonem, naukowym idolem Younga: w reakcji na Principia w XVII w. dość często powtarzał się ni to zarzut, ni to pobłażliwa ocena, iż jest to czysta matematyka, a zatem nie odnosi się wprost do naszego niedoskonałego świata i nie musimy sobie tym zawracać głowy, tym bardziej że matematyka trudna. Young ulegał tu jednak przesądowi, i to podwójnemu. Pierwszy typowy dla wyspiarzy polegał na unikaniu jak ognia wszelkich zapisów algebraicznych i prowadzeniu rozumowań słowami. Była to maniera szkodliwa i niemądra, opóźniająca import kontynentalnej matematyki na Wyspy. W Cambridge mniej więcej od początku wieku działało już Analytical Society, które stawiało sobie za cel zapoznanie studentów z europejskim dorobkiem i pozbycie się zapóźnienia wywołanego zapatrzeniem w bardzo osobiste, idiosynkratyczne podejście do analizy stosowane przez Isaaca Newtona. Drugi przesąd Younga polegał na niedocenianiu wagi matematyki w fizyce. Zdrowy rozsądek jest owszem cenny, ale niebyt daleko prowadzi. Historia fizyki pokazuje, że najbardziej zaawansowana i pozornie odległa od rzeczywistości doświadczalnej matematyka nie tylko znajduje zastosowanie, ale często okazuje się niezbędna. Żeby zrozumieć wszechświat, potrzebna jest geometria riemannowska, żeby zrozumieć właściwości materiałów wokół nas, potrzebna jest mechanika kwantowa rozgrywająca się przecież w zespolonych przestrzeniach Hilberta, a nie w przestrzeni naszych bezpośrednich doświadczeń.
Jeszcze za życia Thomasa Younga falowa teoria światła została niezależnie odkryta i rozwinięta w algebraicznej kontynentalnej postaci. Dokonał tego Augustin Fresnel, który potrafił połączyć solidną matematykę z École polytechnique z inżynierską precyzją eksperymentów. Taka właśnie matematyczna optyka falowa zdominowała cały wiek XIX. Zastosowanie do tęczy zawdzięczamy jednak paradoksalnie Anglikowi, astronomowi George’owi Biddellowi Airy’emu. Objął on z czasem stanowisko Astronoma Królewskiego. Był człowiekiem niezwykle pracowitym i systematycznym. Jego biograf opowiada z uznaniem, iż potrafił spędzić całe popołudnie na wypisywaniu etykietek z napisem „puste” w celu odróżnienia pudełek wypełnionych od pustych. Zapisał się w historii tym, że udało mu się nie spotkać w roku 1845 z Johnem Couchem Adamsem. Raz Airy był we Francji, miesiąc później nie było go w domu, Adams zostawił kartkę i wrócił po godzinie, by usłyszeć, że teraz Astronom Królewski je obiad i się z nim nie spotka. Chodziło zaś o odkrycie kolejnej za Uranem planety. Zirytowany Adams przestał nachodzić Airy’ego, planetę odkryto dzięki obliczeniom nie Adamsa, lecz Francuza Le Verriera. Oprócz tej prestiżowej wpadki cierpliwy i dobrze wykształcony Airy zrobił co najmniej dwie rzeczy pamiętane przez potomność: obliczył dyfrakcyjną zdolność rozdzielczą teleskopu, a także rozkład natężeń w tęczy na podstawie teorii falowej. Pokażemy krótko, jak to się robi.
Promienie świetlne w pobliżu krawędzi tęczy zachowują się tak, jakby pochodziły z wygiętego w kształcie S czoła fali (promienie są bowiem prostopadłe do czoła fali). Wygląda to tak na współczesnym rysunku.

Obrazek za: H.C. van de Hulst, Light Scattering by Light Particles.
Czoło fali jest prostopadłe do promieni, promień wychodzący z O odpowiada maksymalnemu odchyleniu  , promienie wychodzące z P i R jakiejś bliskiej wartości kąta
, promienie wychodzące z P i R jakiejś bliskiej wartości kąta  . Kształt powierzchni falowej jest krzywą trzeciego stopnia, czyli można go zapisać w postaci
. Kształt powierzchni falowej jest krzywą trzeciego stopnia, czyli można go zapisać w postaci

gdzie  jest bezwymiarowym współczynnikiem, a promień kropli w mianowniku musi być w kwadracie, żeby zgadzały się jednostki, trójka jest tu dla wygody. Współczynnik ten nietrudno obliczyć (*), choć nie jest szczególnie istotny, w każdym razie dopóki nie porównujemy teorii z eksperymentem bądź obserwacją tęczy. Promienie docierające pod kątem
jest bezwymiarowym współczynnikiem, a promień kropli w mianowniku musi być w kwadracie, żeby zgadzały się jednostki, trójka jest tu dla wygody. Współczynnik ten nietrudno obliczyć (*), choć nie jest szczególnie istotny, w każdym razie dopóki nie porównujemy teorii z eksperymentem bądź obserwacją tęczy. Promienie docierające pod kątem  mają różnicę fazy wynikającą z kształtu czoła fali oraz z kąta obserwacji. Różnica faz odpowiadająca odległości RQ jest równa
mają różnicę fazy wynikającą z kształtu czoła fali oraz z kąta obserwacji. Różnica faz odpowiadająca odległości RQ jest równa

Sumując wszystkie fale  dla różnych wartości
dla różnych wartości  , czyli całkując otrzymujemy zespoloną amplitudę fali obserwowanej pod danym kątem proporcjonalną do
, czyli całkując otrzymujemy zespoloną amplitudę fali obserwowanej pod danym kątem proporcjonalną do

Tutaj 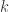 oznacza
oznacza  . Rozszerzyliśmy granice całkowania do nieskończoności, ponieważ sądzimy, iż funkcja w wykładniku urojonym oscyluje coraz szybciej i nie wniesie istotnego wkładu dla dużych
. Rozszerzyliśmy granice całkowania do nieskończoności, ponieważ sądzimy, iż funkcja w wykładniku urojonym oscyluje coraz szybciej i nie wniesie istotnego wkładu dla dużych  . Okazuje się też rzeczywista, ponieważ wykładnik jest nieparzystą funkcją
. Okazuje się też rzeczywista, ponieważ wykładnik jest nieparzystą funkcją  . Ostatecznie natężenie, jakiego możemy oczekiwać po zsumowaniu wszystkich fal będzie proporcjonalne do kwadratu amplitudy, czyli kwadratu całki
. Ostatecznie natężenie, jakiego możemy oczekiwać po zsumowaniu wszystkich fal będzie proporcjonalne do kwadratu amplitudy, czyli kwadratu całki

gdzie

Airy obliczył tę całkę numerycznie, co nie jest zadaniem banalnym: najpierw trzeba ją obliczyć na jakimś odcinku skończonym, a później znaleźć przybliżenie dla reszty aż do nieskończoności. Praca ta musiała go kosztować bardzo dużo wysiłku, wykonał ją porządnie, zamieścił tabelki funkcji w swoim artykule. Z oczywistych powodów nazywa się ona funkcją Airy’ego. Spotyka się ją także w mechanice kwantowej dla potencjału opisywanego funkcją liniową (por. np. L.D. Landau i E. M. Lifszyc, Mechanika kwantowa).

Airy porównał swoje wyniki dla tęczy z teorią Descartes’a i Younga. Widzimy, że maksima Younga są wyraźnie przesunięte w stosunku do teorii falowej. Tak czy owak teoria Younga jest zbyt prosta matematycznie i nie opisuje złożoności sytuacji. Jej główny brak jest właśnie matematyczny: zamiast dwóch promieni trzeba uwzględnić nieskończenie wiele fal. Nie darmo wprowadzono całkowanie jako swoiste uogólnienie sumowania. Teoria Airy’ego przewiduje też, że pierwsze maksimum tęczy leży nieco wewnątrz łuku Descartes’a (oś pionowa na rysunku). Więcej konkretnych wyników pokazałem tutaj. Oczywiście, także teoria Airy’ego jest przybliżona, choćby z powodu rozszerzenia całkowania do nieskończoności w kierunku poprzecznym. Okazuje się jednak, że jest to przybliżenie wyjątkowo skuteczne, gdy chcemy zrozumieć, co się dzieje.
A to obrazki funkcji Airy’ego i jej kwadratu, czyli u nas natężenia światła w pobliżu krawędzi tęczy.


W mechanice kwantowej funkcja Airy’ego to funkcja falowa w polu jednorodnym: z prawej strony mamy zanikającą wykładniczo część „tunelową”, odpowiadającą ujemnej energii kinetycznej, z lewej strony coraz szybsze oscylacje odpowiadające coraz większej energii kinetycznej cząstki. Kwadrat funkcji falowej opisuje gęstość prawdopodobieństwa i jak to w mechanice kwantowej cząstka ma niezerowe prawdopodobieństwo znalezienia się w obszarze klasycznie zabronionym, gdzie energia kinetyczna jest ujemna. W przypadku tęczy  jest proporcjonalne do odległości kątowej od krawędzi tęczy geometrycznej – odpowiada jej oś pionowa. Ponieważ jest to teoria falowa, więc fale wnikają nawet tam, gdzie klasycznie jest to zabronione (prawa część wykresu dla
jest proporcjonalne do odległości kątowej od krawędzi tęczy geometrycznej – odpowiada jej oś pionowa. Ponieważ jest to teoria falowa, więc fale wnikają nawet tam, gdzie klasycznie jest to zabronione (prawa część wykresu dla  ). Pierwsze maksimum leży nieco wewnątrz tęczy Descartes’a, pojawiają się także kolejne, coraz bliżej siebie. Young był blisko prawdy, jeśli chodzi o położenie maksimów natężenia w tęczy jego warunek na różnicę dróg optycznych należy zmodyfikować do postaci
). Pierwsze maksimum leży nieco wewnątrz tęczy Descartes’a, pojawiają się także kolejne, coraz bliżej siebie. Young był blisko prawdy, jeśli chodzi o położenie maksimów natężenia w tęczy jego warunek na różnicę dróg optycznych należy zmodyfikować do postaci

Nadal nie jest to dokładnie to samo co w teorii Airy’ego, ale dość blisko. Źródło tej dodatkowej różnicy faz można wyjaśnić, lecz wyjaśnienie wymaga dodatkowego wysiłku matematycznego, którego tu nie podejmiemy.
Gustav Mie już na początku wieku XX obliczył, jak wygląda rozpraszanie fali elektromagnetycznej na dielektrycznej kuli, co obejmuje interesujący nas przypadek. Wynik ma postać rozwinięcia nieskończonego i choć jest ścisły nie bardzo pozwala coś zobaczyć po drodze między wejściem a wyjściem, wymaga uwzględnienia tysięcy wyrazów, czyli komputera. Stosowano też do zagadnienia tęczy zespolone momenty pędu, ale nie jestem przekonany, czy problem stał się przejrzystszy. Inaczej mówiąc, panujemy nad nim rachunkowo, ale czasem jest to tylko zwycięstwo numeryczne, a zatem ograniczone.
(*) Zobaczmy jeszcze, jak znaleźć współczynnik h. Kąt odchylenia promienia dla pierwszego łuku tęczy dany jest wzorem

gdzie  . W okolicy ekstremalnego odchylenia otrzymamy
. W okolicy ekstremalnego odchylenia otrzymamy

Tutaj  jest drugą pochodną
jest drugą pochodną  wziętą w ekstremum. Patrząc na rysunek powyżej, mamy
wziętą w ekstremum. Patrząc na rysunek powyżej, mamy

Po scałkowaniu dostaniemy wynik.










 Na rysunku Huygensa promienie światła/płaska fala świetlna padają pionowo od dołu. Fala odbija się od okręgu ABC, tworząc kaustykę AFNE.
Na rysunku Huygensa promienie światła/płaska fala świetlna padają pionowo od dołu. Fala odbija się od okręgu ABC, tworząc kaustykę AFNE.

z osią
. Zatem równanie promienia odbitego to
. Różniczkując to równanie po
przy stałych wartościach
otrzymamy równanie zawierające tylko zmienną
, z którego
:
. Szukamy przecięcia dwóch bliskich krzywych z rodziny, czyli
, otrzymujemy pochodną
.