Let me here remind you that the essence of dramatic tragedy is not unhappiness. It resides in the solemnity of the remorseless working of things. This inevitableness of destiny can only be illustrated in terms of human life by incidents which in fact involve unhappiness. For it is only by them that the futility of escape can be made evident in the drama. This remorseless inevitableness is what pervades scientific thought. The laws of physics are the decrees of fate.
„… istotą [greckiej] tragedii nie jest nieszczęście. Istotą jej jest powaga bezlitosnego działania rzeczy. W kategoriach życia ludzkiego nieuchronność przeznaczenia ilustrować mogą jedynie przypadki, które w rzeczywistości pociągają za sobą nieszczęście. Bowiem tylko w ten sposób można w dramacie ukazać daremność ucieczki. Myśl naukową przenika taka właśnie bezlitosna konieczność. Prawa fizyki to wyroki losu.” [A.N. Whitehead, przeł. M. Kozłowski, M. Pieńkowski]
Żyjemy w pożyczonym czasie. Wystarczy odrobina szaleństwa po którejś stronie Atlantyku i w ciągu paru godzin z Ameryki Północnej, Europy od Lizbony po Ural i jeszcze dalej zostaną radioaktywne zgliszcza. Pewnie ludzkość by to przetrwała jako gatunek biologiczny, może Chiny mogłyby wreszcie zapanować nad światem, jak marzy się Generalnemu Sekretarzowi Xi. Byłoby to jednak ponure zwieńczenie czterech wieków nauki nowożytnej: od Keplera i Galileusza do Feynmana, Weinberga, Salama, Glashowa, Grossa, Politzera, Wilczka i ‚t Hoofta. Zbudowanie i użycie bomby atomowej stało się symbolicznym początkiem ery nuklearnej, a także początkiem Stanów Zjednoczonych w roli supermocarstwa dominującego w światowej polityce. Jak do tej pory pierwotny zamysł, aby wyprodukować tę potworną broń szybciej, niż zrobią to naziści/komuniści, sprawdził się. Gdyby nie militarna dominacja Stanów Zjednoczonych, broni jądrowej użyto by już dawno na mniejszą albo raczej na większą skalę.
Znakomity film Christophera Nolana przypomniał dramat Roberta Oppenheimera, jednego z bohaterów amerykańskiej wyobraźni. Nie sądziłem, że można zrobić wysokobudżetowy film dla masowej widowni, upraszczając tak niewiele i wkładając tak wiele informacji historycznej i psychologicznej. (Wątek Einsteina brzmiał dość fałszywie: nikt by się nie zwracał do Einsteina w sprawie obliczeń Hansa Bethego dotyczących fizyki jądrowej, jeśli już to do Fermiego czy Szilarda; prawdziwe natomiast jest to, że Einstein niezbyt rozumiał, czemu Oppenheimer daje się upokarzać jakimś komisjom, jeśli nie musi. On sam nie wierzył w państwo jako instytucję, nie miał zbyt wielu złudzeń, choć uważał państwo amerykańskie za znacznie lepsze od swoich ojczystych Niemiec. Dlatego zresztą nawet nie myślał o powrocie do Niemiec po wojnie. Nb. ci agenci FBI grzebiący w śmieciach i podsłuchujący telefony to była rzeczywistość nie tylko Oppenheimera, ale i Einsteina, choć ten żadnych „tajemnic atomowych” nie znał ani nie chciał znać.)
Sprawa Oppenheimera była z pozoru intrygą biurokratyczną: wyznaczona arbitralnie komisja, działająca w sposób inkwizytorski, odmówiła uczonemu certyfikatu dostępu do tajemnic wojskowych i państwowych. W ten sposób jeden z największych patriotów amerykańskich odsunięty został od wpływu na decyzje w sprawach broni nuklearnej. W roku 1954 był to szok dla opinii publicznej, Oppenheimer znany był bowiem jako dyrektor programu budowy bomby atomowej w Los Alamos, jego sława przyćmiła nawet Einsteina. Zbombardowanie Hiroszimy i Nagasaki przyspieszyło kapitulację Japonii i koniec wojny, tak przynajmniej powszechnie wierzono. Oppenheimer stał się ikoną życia publicznego, twarzą amerykańskiej nauki, wierzono, że jest supergeniuszem. Nie był nawet szeregowym geniuszem, lecz umiejętnie kierował ludźmi od siebie znacznie wybitniejszymi, jak Isidor Rabi, Hans Bethe, Enrico Fermi, Richard Feynman, Rudolf Peierls, John von Neumann, Stanisław Ulam, a także Edward Teller – enfant terrible Programu Manhattan, obsesyjny zwolennik broni termojądrowej, chimeryczny i paranoiczny węgierski teoretyk niepasujący do żadnego zespołu ludzi, pełen jednak pomysłów, których ogromna większość była do niczego, ale kilka okazało się dobrych. W Projekcie Manhattan Teller był na uboczu, snując wizje broni termojądrowej.
Aż do roku 1951, do projektu Tellera-Ulama, bomba termojądrowa była tylko umykającym marzeniem Tellera bez realnej nadziei na sukces. Koła wojskowe naciskały, by realizować ten projekt nawet kosztem realnego programu budowy bomb rozszczepialnych. Nie chodziło tylko o podział wydatków, ale i decyzje, co produkować w reaktorach: więcej plutonu do bomb rozszczepialnych, czy trytu do superbomby Tellera. Decyzja polityczna podjęta została w roku 1949, gdy nie było żadnego realnie działającego pomysłu bomby termojądrowej. To, że gwiazdy potrafią syntetyzować wodór w hel, jest wskazówką niezbyt pomocną z technicznego punktu widzenia. Wiadomo było, że należy jakoś wykorzystać wybuch bomby rozszczepialnej, by stworzyć ekstremalnie wysoką temperaturę potrzebną do rozpoczęcia syntezy jąder. Jak jednak sprawić, żeby doszło do podtrzymującej się reakcji, zanim energia wybuchu rozproszy się w otoczeniu, nikt nie wiedział. Oppenheimer nie był entuzjastą superbomby z tego i z innych powodów. Zapowiadało się, że będzie to konstrukcja gigantyczna. Trzeba by ją wozić wołami na miejsce wybuchu, pierwsza amerykańska bomba Ivy Mike to było całe laboratorium z ciekłym deuterem wysadzone zdalnie w powietrze, nie było mowy o transportowaniu tego w całości w bezpieczny sposób nawet na okręcie. Istniała też wątpliwość strategiczna: czy wojsko może sensownie użyć bomby niszczącej nie tylko jedno miasto, ale i cały kilkudziesięciokilometrowy okręg wokół tego miasta. To jest niewątpliwie broń masowego ludobójstwa, żadne cele militarne tego nie usprawiedliwiają. Stanowisko Oppenheimera nie było zresztą pacyfistyczne, przeciwstawiał się on raczej entuzjastycznej postawie kół wojskowych, które sprowadzały rzecz do tego, kto będzie miał silniejsze bomby, nie wątpiąc ani na chwilę, że zawsze będą to Amerykanie. To się nie sprawdziło. Rosjanie mieli fizyków i zasoby, żeby zbudować sobie taką broń. Korzystali z informacji szpiegowskich, ale i bez nich historia wyglądałaby tak samo, dwa lata wcześniej, czy później nie miało tu żadnego znaczenia.
Oppenheimer miał przeciwników i wrogów. Teller doszukiwał się wpływów Oppenheimera w każdej decyzji, która była nie po jego myśli. Kompleks niższości wobec Oppenheimera żywił Lewis Strauss, sprzedawca butów, który dorobił się milionów na inwestycjach i po wojnie został admirałem, choć przesiedział ten okres w biurach zaopatrzenia (złośliwi nazywali go „admirałem holowników”). Strauss pełnił różne funkcje w administracji waszyngtońskiej i szczerze znienawidził Oppenheimera za arogancję, co racjonalizował w podejrzeniach o szpiegostwo (składał też donosy, że Oppenheimer nie rozlicza się uczciwie z powierzonych funduszy). Rozpowiadał też, że Oppenheimer miał romans z Ruth Tolman, żoną znakomitego fizyka Richarda Tolmana z Caltechu i że sprawa ta przyspieszyła śmierć Richarda, co było paskudną plotką. Strauss nie dość, że nie skończył szkoły średniej i pieniądze miał w pierwszym pokoleniu, był bardzo religijnym Żydem i ktoś taki jak Oppenheimer: bogaty od urodzenia, właściciel van Goghów i Corotów, znający się nie tylko na kwestiach naukowych, ale i na sztuce, literaturze, w dodatku podobający się kobietom, będący w jego pojęciu niemoralnym ateistą, zdrajcą swej religii i tradycji, niemal na pewno był sowieckim szpiegiem. Gdzieś w ukryciu był J. Edgar Hoover, szef FBI, który śledził wszystkich, marzył, aby odebrać obywatelstwo amerykańskie Einsteinowi (za rzekomą działalność komunistyczną) i miał na oku na Oppenheimera jeszcze od lat czterdziestych. Gotów był zaakceptować i prowadzić każdy wątek w tym śledztwie: nawet podejrzenie, że uczony był homoseksualny (nie był; to Hoover był homoseksualistą, do czego zgodnie z ciągle żywą prawicową tradycją nigdy się nie przyznał).
Strauss jako przewodniczący Komisji Energii Atomowej (AEC) postanowił odebrać Oppenheimerowi poświadczenie bezpieczeństwa. Wygasało ono wprawdzie automatycznie w połowie roku 1954, chodziło jednak o to, by odebrać je wcześniej i upokorzyć uczonego. Oznaczało to także, że Oppenheimer nie będzie konsultantem nie tylko w AEC, ale i we wszystkich agencjach i komitetach rządowych. Skład trzyosobowej specjalnej komisji prowadzącej postępowanie (Personnel Security Board, PBS) w sprawie poświadczenia bezpieczeństwa wybrał Strauss, on także wybrał prawnika prowadzącego postępowanie, agresywnego specjalistę od przesłuchań Rogera Robba. FBI zapewniła podsłuchy codziennych konsultacji Oppenheimera i jego prawników, tak że Strauss na bieżąco kontrolował przebieg postępowania, znając rozmowy i nastroje strony przeciwnej. Przygotowywał też świadków, np. Edward Teller powtórzył tylko przed komisją to, co wcześniej uzgodnił ze Straussem. Obrona nie miała dostępu do tajnych materiałów, Robb mógł więc łapać Oppenheimera na nieścisłościach w jego wypowiedziach sprzed dwunastu lat podsłuchanych przez FBI. Uczonemu nie udostępniono tych taśm, musiał więc wierzyć na słowo, że mówił to, co mówił.
Oppenheimer miał polityczną przeszłość, która mobilizowała agentów do grzebania w poszukiwaniu podejrzanych kontaktów. W latach trzydziestych i na początku czterdziestych wśród jego znajomych, studentów, doktorantów, przyjaciół i kochanek pełno było komunistów. Członkiem partii komunistycznej był także jego młodszy brat Frank. Do dziś spekuluje się, czy Robert Oppenheimer był członkiem partii komunistycznej, czy nie. Jest to trochę talmudyczna dyskusja, rozstrzygnęłoby ją może dopiero znalezienie legitymacji członkowskiej Oppenheimera. Bez wątpienia sympatyzował z lewicą, ale w Kalifornii przed wojną nie musiało to oznaczać działania na rzecz państwa sowieckiego. Oppenheimer, podobnie jak Jean Tatlock, jego kochanka, córka profesora literatury w Berkeley, byli raczej kawiorową lewicą, ludźmi uprzywilejowanymi, którzy nie chcieli, aby te przywileje dostępne były jedynie wybrańcom losu. Kto nie był za młodu lewicowy, ten na starość staje się świnią. Nie było nigdy dowodów, aby Robert Oppenheimer był lojalny wobec jakiegokolwiek innego państwa poza swoim własnym. Czuł się stuprocentowym amerykańskim patriotą i pragnął pomóc własnemu krajowi, a także światu, wygrać wojnę światową. Rosjanie aż do końca wojny byli zresztą sojusznikami Zachodu – z tego powodu nie można było skazać Klausa Fuchsa na więcej niż czternaście lat, jego szpiegostwo nie dotyczyło bowiem kraju wrogiego.
W roku 1954 nie było żadnych informacji, które nie byłyby znane w roku 1947, kiedy to przedłużono Oppenheimerowi dostęp do tajemnic. Wcześniej oczywiście był projekt Manhattan, wtedy pomimo zastrzeżeń służb generał Leslie Groves zadecydował, że uczony ma otrzymać poświadczenie bezpieczeństwa, ponieważ jest zbyt ważny dla całego programu. Groves miał rację, bez Oppenheimera, który potrafił zmotywować swoim entuzjazmem i zaangażowaniem wszystkich pracujących nad projektem, od noblistów i przyszłych noblistów aż po sekretarki i kobiety zatrudnione do obliczeń na arytmometrach jako „human computers”, Projekt Manhattan nie powiódłby się w tak krótkim czasie. Pod koniec prac Oppenheimer ważył 52 kg przy wzroście 178 cm. Udało się jednak w ciągu dwóch lat zaprojektować i zbudować nie jeden, ale dwa rodzaje bomb rozszczepialnych: uranową i plutonową. Przy czym w przypadku tej drugiej trudności techniczne były ogromne i jeszcze pod koniec roku 1944 nie było pewności, czy się uda. Pluton jest bowiem najpierw ściskany energią implozji, co zapoczątkowuje reakcję łańcuchową. Jak na ironię, mechanizmami implozji zajmował się m.in. Klaus Fuchs, niemiecki fizyk, który dołączył do programu ze strony brytyjskiej. Był ważnym członkiem zespołu, zaraz po wojnie wraz z Johnem von Neumannem zgłosił tajny patent na zapłon reakcji termojądrowej za pomocą implozji materiału rozszczepialnego – był to już wstęp do prac nad bombą termojądrową. Fuchs uchodził za jednego z najzdolniejszych teoretyków w projekcie Manhattan. Nikt się nie domyślał, że ma jedną wadę: jest fanatycznym komunistą i przekaże informacje Sowietom. Oczywiście służby wytrwale szczekały nie pod tym drzewem. Identyfikacja Fuchsa okazała się możliwa dopiero po wojnie dzięki projektowi Venona, wytrwałej pracy nad rozszyfrowywaniem sowieckich depesz. Sukces ten był głównie dziełem kobiet zatrudnionych w tym żmudnym projekcie, a nie dzielnych agentów FBI podsłuchujących i śledzących podejrzane kontakty lewicowych uczonych.
Komisja drążyła głównie dwie kwestie: wątek Eltentona i niechętny stosunek do superbomby. Ten pierwszy problem stworzył sobie sam uczony, informując w połowie roku 1943 służby wojskowe, że niejaki George Eltenton, inżynier pracujący w Shell Oil, w imieniu Rosjan próbował szukać kontaktu z uczonymi związanymi z programem atomowym. Oppenheimer mówił o trzech takich próbach i nie chciał wymienić żadnych nazwisk. Służby, zarówno wojskowe, jak i FBI, przez następne lata bezskutecznie próbowały ustalić, kto był tym pośrednikiem i do kogo się zwracano. Ostatecznie okazało się, że chodziło jeden taki przypadek, o rozmowę w kuchni między Oppenheimerem a Haakonem Chevalierem, profesorem romanistyki z Berkeley. Chevalier poinformował Oppenheimera, że Eltenton ofiarowywał się jako pośrednik w przekazaniu informacji o programie Rosjanom. Oppenheimer uciął rozmowę, uważając, że byłaby to zdrada. Nie wydarzyło się nic więcej. Wzmianka o trzech osobach była niepotrzebnym kłamstewkiem, mającym zapewne odwrócić uwagę od faktu, że chodziło o samego Oppenheimera. Epizod ten wydarzył się na początku roku 1943, kiedy było bardzo niewiele „tajemnic atomowych”, nie powstał jeszcze ośrodek w Los Alamos, nie zaczęła się na serio praca nad rozdzielaniem izotopów uranu, zaledwie miesiąc wcześniej zaczął działać eksperymentalny reaktor jądrowy w Chicago. Naiwność/głupota Oppenheimera sprawiła, że epizod z Chevalierem znalazł się w polu zainteresowania służb. Wracano do tego w trakcie projektu Manhattan, a także po wojnie. Sprawę tę rozdęto do ponadnaturalnych rozmiarów w roku 1954, uznając, że świadczy o niefrasobliwym podejściu do kwestii bezpieczeństwa. Innym argumentem było spotkanie z Jean Tatlock w roku 1943, które dla śledzących uczonego agentów było co najmniej podejrzane, Tatlock była bowiem komunistką i w spotkaniu tym upatrywano potencjalnego kontaktu z Rosjanami. W rzeczywistości w tym czasie Tatlock nie interesowała się polityką, była lekarzem-psychiatrą i cierpiała na depresję. Niedługo później popełniła samobójstwo i nie miało to nic wspólnego z polityką, lecz najprawdopodobniej z jej orientacją seksualną (nawet lekarze sądzili wówczas, że homo czy biseksualizm jest chorobą). Wyciągnięto ten epizod prawdopodobnie także dlatego, żeby w trakcie przesłuchań dowiedziała się o nim Kitty Oppenheimer, żona uczonego, może liczono na to, że rozgniewana tymi rewelacjami ujawni coś kompromitującego na temat męża. Oppenheimer rzeczywiście kręcił w sprawie Eltentona, choć trzeba też stwierdzić, że to przez jego skrupuły zaistniał cały ów problem. Gdyby Oppenheimer nie wspomniał o Eltentonie, służby nic by o tym epizodzie nie wiedziały. Uczony chciał zapewne chronić tożsamość Chevaliera, ale później, pod naciskiem wyjawił nazwisko Chevaliera Grovesowi, a w 1946 roku FBI. Chevalier stracił posadę w Kalifornii i po kilku latach życia na marginesie udało mu się wyjechać do Francji (miał także obywatelstwo francuskie).
Niechętny stosunek do superbomby dziś brzmi raczej jak głos rozsądku. W tamtym czasie wojsko chciało mieć wszystko atomowe: samoloty, statki, działa. Chciano zarazem silniejszych bomb, ale i słabszych, które mogłyby się przydać na froncie. Lotnictwo uważało, że Oppenheimer działa na rzecz marynarki, twierdząc, iż nie będzie samolotów z napędem nuklearnym. W ogóle armia amerykańska była cichym uczestnikiem tego postępowania przeciwko Oppenheimerowi, o czym film Nolana prawie nie wspomina. Warto też pamiętać, że Oppenheimer po wojnie i po Hiroszimie nie był jakimś nawiedzonym pacyfistą, który chciał z wujkiem Stalinem pod rękę zaprowadzić wieczny pokój. Zdawał sobie sprawę, jak wygląda reżim sowiecki, jego bliskim przyjacielem był George Kennan, architekt zimnej wojny. Starał się jednak szukać szansy na powstrzymanie wyścigu zbrojeń, może naiwnie, ale wojny nuklearnej powinniśmy się obawiać także i dziś (co wcale nie znaczy, iż należy np. ustępować przed rosyjskim szantażem). Podejście uczonego do spraw broni nuklearnej było złożone, zmieniało się też z czasem i sytuacją. Ktoś napisał, że film „Oppenheimer” pokazuje, iż łatwiej być fizykiem niż politykiem. Cóż, i tak, i nie. Obie dziedziny niosą inny rodzaj trudności. Uczony wiedział, jak trudno być naprawdę twórczym fizykiem: znał Heisenberga, Pauliego, Bohra, Fermiego, Diraca i musiał czuć się przy nich chwilami jak Strauss przy Oppenheimerze. Był za inteligentny na to, żeby nie dostrzegać różnicy między kimś wszechstronnie uzdolnionym a geniuszem. Polityka jest sztuką zarządzania ludźmi i ich emocjami, co może wydawać się czasem trudniejsze niż powstrzymanie reakcji łańcuchowej w uranie. Z pewnością Oppenheimer nie był człowiekiem prostym i politycznie naiwnym, ale nie był też cynikiem i dlatego całe to dochodzenie w sprawie dostępu do tajemnic złamało go. Wynikiem postępowania nie było zresztą odebranie głosu fizykom, ale oddanie go Edwardowi Tellerowi, też fizykowi, tyle że dość paranoidalnemu. Oppenheimer wycofał się z życia publicznego, pilnował się, żeby nie wypowiadać się na żadne drażliwe tematy. Jego przeciwnicy sądzili, że może uciec do Związku Sowieckiego, choć jemu nawet Europa zachodnia wydawała się obcym światem, mimo tego, że znał języki, literaturę, miał przyjaciół.
Być może w naturze ludzkiej leży, by nie rezygnować ze zdobycia tego, co jest możliwe, nawet gdy czujemy, jakie to niebezpieczne. Oppenheimer miał daleko posunięte upodobanie do sytuacji granicznych i niebezpiecznych. Ludzie, którzy jeździli z nim po Nowym Meksyku konno, wspominali to często jako doświadczenie ekstremalne. Koń Oppenheimera nauczony był kłusować tak, aby zawsze tylko jednym kopytem dotykać ziemi, dzięki czemu i on, i jeździec radzili sobie w najtrudniejszym terenie, w nocy, podczas burzy. Być może ludzkość skazana jest na najgorsze, na rządy kolejnych wujków Stalinów i Putinów, paranoicznych miłośników tajnych służb i realpolitik, ale może jednak jest jeszcze jakaś nadzieja, że nie tylko złe prognozy muszą się spełniać.








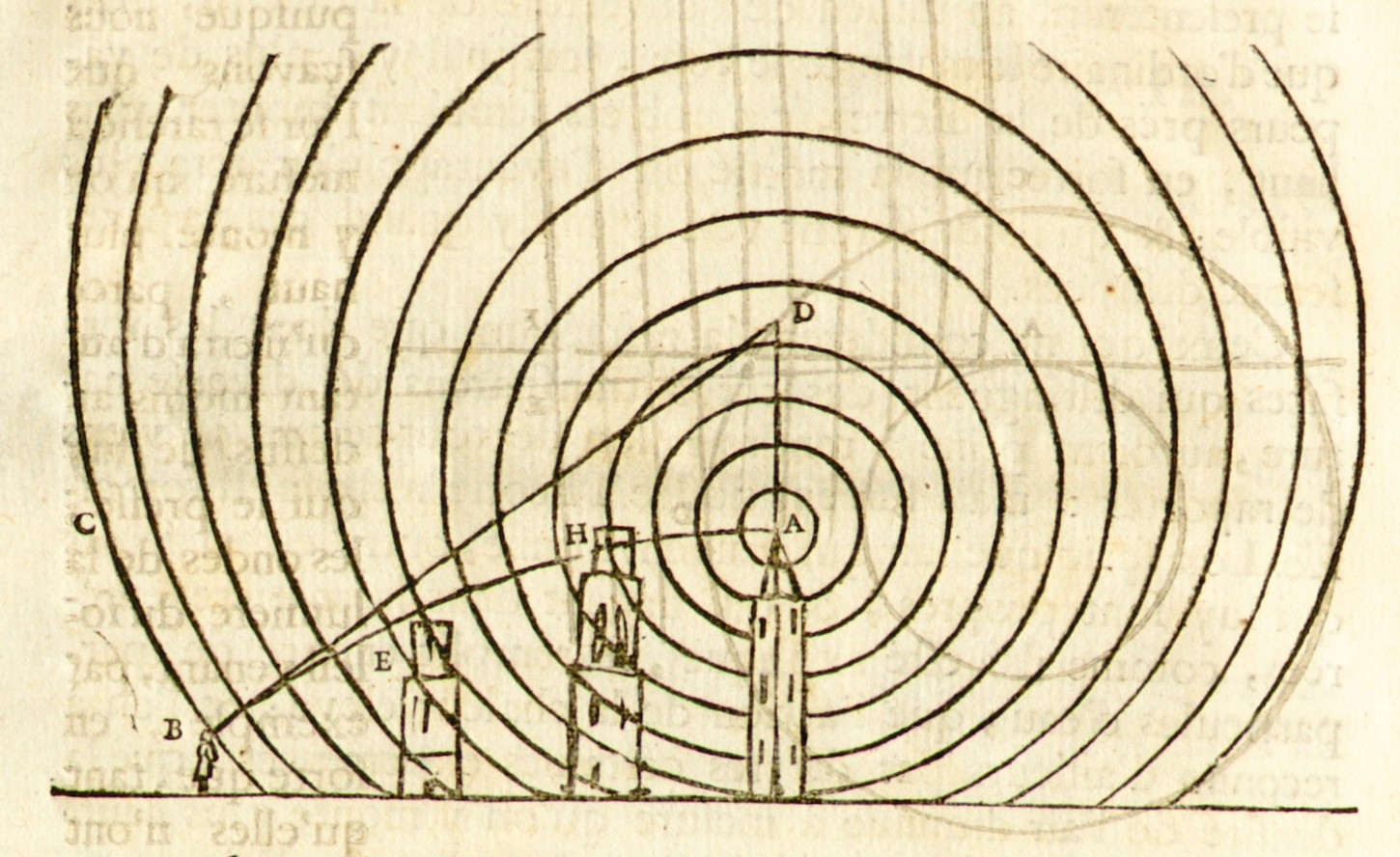
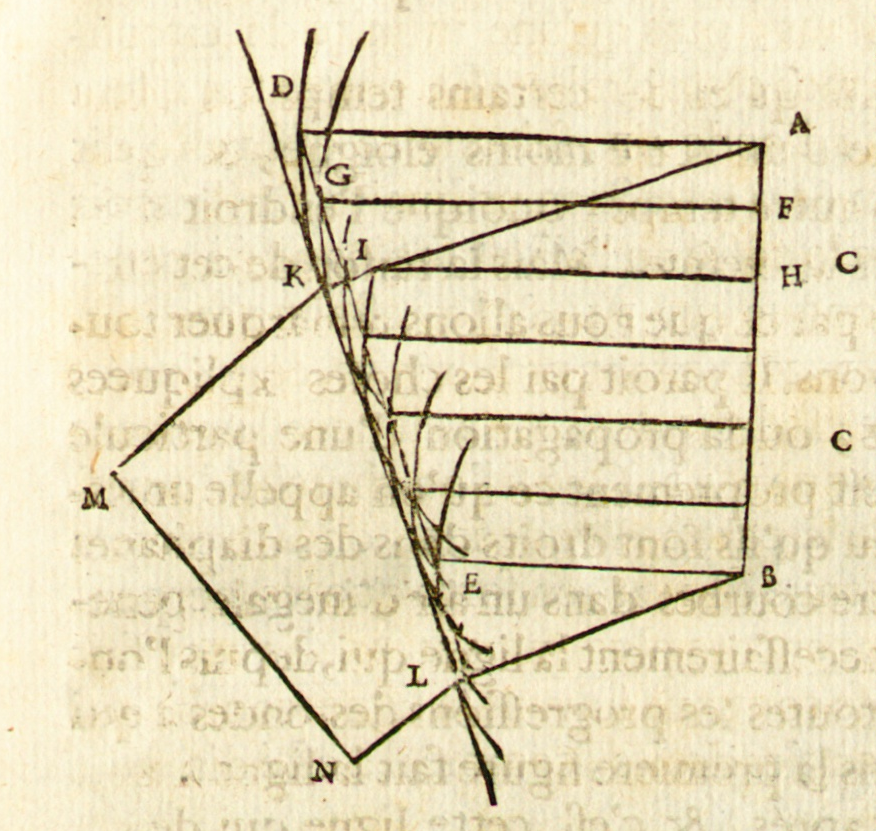



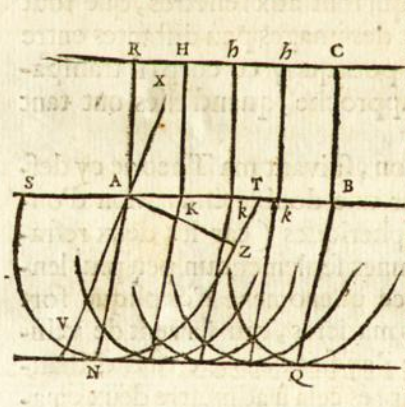
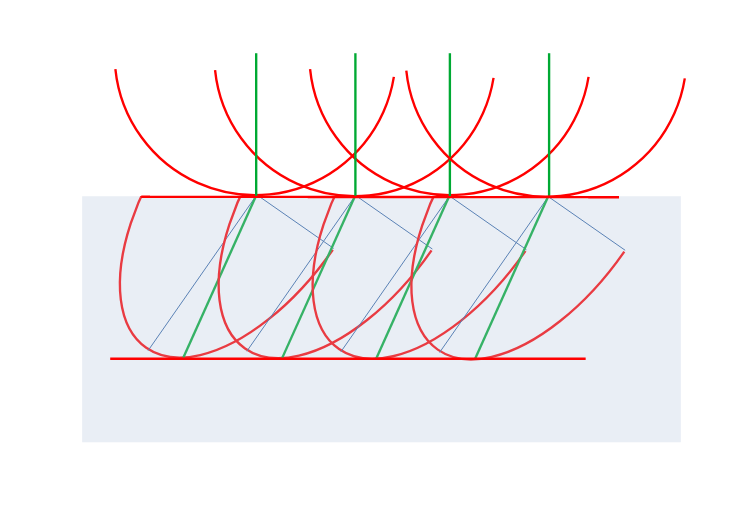






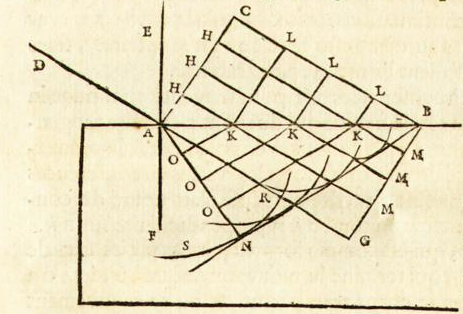




 Na rysunku Huygensa promienie światła/płaska fala świetlna padają pionowo od dołu. Fala odbija się od okręgu ABC, tworząc kaustykę AFNE.
Na rysunku Huygensa promienie światła/płaska fala świetlna padają pionowo od dołu. Fala odbija się od okręgu ABC, tworząc kaustykę AFNE.