Ponieważ pisałem o spiralach u van Gogha, więc może warto napisać trochę więcej o ich matematyce. Zdefiniujmy spiralę jako krzywą, która zawsze tworzy kąt z promieniem wodzącym z początku układu.
Najłatwiej równanie spirali zaleźć we współrzędnych biegunowych: położenie punktu określamy przez odległość od początku układu oraz kąt
, jaki tworzy promień wodzący z ustaloną półosią. Kąty liczymy przeciwnie do wskazówek zegara. Wielkim odkryciem XVII wieku w matematyce było zauważenie, że krzywe gładkie można traktować jak złożone z bardzo krótkich odcinków linii prostych, najlepiej nieskończenie małych odcinków (ale zawsze można sobie wyobrażać coraz mniejsze odcinki skończone). Narysujmy sobie taki nieskończenie mały odcinek spirali. Oczywiście, musimy narysować odcinek skończony (niebieski na rysunku), nieskończenie małe wielkości nie nadają się do rysowania.
Stałość kąta oznacza, że stały, tj. niezależny od punktu jest także jego cotangens:
Oznaczyliśmy cotangens kąta literą
, żeby mniej pisać. Wielkość ta nie zależy od punktu spirali. Znaczy to, że gdy obracamy wektor wodzący o
, to jego nowa długość równa się
Po dwóch obrotach o dostaniemy
. Gdyby kąt był czasem, a
stopą procentową, to mielibyśmy procent składany: po każdym okresie
nasz kapitał rośnie o stały czynnik
. Sens geometryczny tej spirali jest więc łatwy do uchwycenia: każdy obrót o ustalony kąt oznacza wzrost promienia o ustalony procent, czyli o ustalony czynnik. Wzrost jest więc wykładniczy. Zaczynając od promienia
przy kącie
, mamy po
obrotach
Skończony kąt możemy uzyskać jako złożenie bardzo wielu obrotów o mały kąt
. Będzie wówczas spełniony warunek
. Promień
będzie równy
gdzie oznacza podstawę logarytmu naturalnego (*). Wykładnicza zależność
oznacza, że obracając się w kierunku ujemnym, nigdy nie otrzymamy zera, a więc nasza spirala nie tylko rozwija się nieskończenie, ale i zwija w pobliżu zera nieskończenie wiele razy. Wynika to po prostu z faktu, że
może przyjmować dowolne wartości rzeczywiste, dodatnie, ujemne (albo zero), a
zawsze będzie dodatnie. Nie można narysować otoczenia początku układu, bo tam spirala zwija się nieskończenie wiele razy.
Łatwo jest też obliczyć długość spirali od punktu początkowego do danego kąta . Patrząc jeszcze raz na nasz nieskończenie mały odcinek spirali, widzimy, że całkowita jej długość jest proporcjonalna do
, a więc skończona:
(*) Możemy sobie wyobrażać, że liczba staje się coraz większa, ale tak aby
. Korzystamy z z granicy przy
:




Nie rozumiem skąd wniosek, że na tym pierwszym wykresie przeciwprostokątna ma długość rdφ. Poza tym, jeśli wierzchołki tego małego trójkąta nazwiemy odpowiednio A (między ds i dr), B (między dr i rdφ) i C (między rdφ i ds), to jeśli kąt przy wierzchołku B ma kąt prosty, to odcinek od początku układu współrzędnych do wierzchołka C jest przecież różny od odcinka r+dr, więc jeśli wierzchołek A leży na spirali, to wierzchołek C nie leży na spirali. Proszę o wyjaśnienie.
PolubieniePolubienie
Chodzi o nieskończenie mały trójkąt. którego przeciwprostokątną jest , a przyprostokątnymi
, a przyprostokątnymi 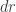 oraz
oraz 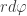 .
.
PolubieniePolubienie
Ale jeśli odległość od wspomnianego wierzchołka C (tego na górze odcinka rdφ) do środka ukł. wsp. jest taka sama jak r + dr, to przecież ten kąt między dr i rdφ wcale nie jest kątem prostym.
PolubieniePolubienie
Chodzi o współrzędne biegunowe; dr i rdφ są prostopadłe z definicji; odcinek, od początku układu do C geometrycznie powinien być trochę dłuższy niż r+dr, ale to nie ma znaczenia, gdy wielkości dr i rdφ dążą do zera (różnica długości obu tych „długich” odcinków OC i OB jest rzędu dr^2, czyli do pominięcia. Zamiast posługiwać się granicami używam nieskończenie małych, jest to dokładnie równoważne.
PolubieniePolubienie